Bilgisayarlardaki aritmetiğin temeli
Bilgisayarın nasıl hesap yaptığını merak ettiniz mi? Tahmin mi ediyorlar? Yoksa içine tüm olası kombinasyonları kodladık mı? Tabii ki de bu iki sorunun cevabı, Hayır.
Hiç bilgisayarların nasıl hesap yaptığını merak ettiniz mi? Çoğu insan bu sorunun cevabı olarak üstü kapalı olarak işlemci deyip geçecektir. Ancak sorunun cevabı bu değildir. Çoğu kişi işlemcileri basitçe çok hızlı hesap makinelerine benzetir. Ancak bu benzetme tam anlamıyla doğru değildir. Bu benzetme işlemcinin içerisindeki ALU (Arithmetic-Logic Unit) için doğru olabilir; fakat işlemcilerin içerisinde sadece ALU bulunmaz. İşlemcilerin içerisinde CU (Control Unit), ALU (Arithmetic-Logic Unit), Registerlar, Önbellek gibi komponentler bulunur.
UYARI: Bu yazıyı anlamanız için temel mantık ve temel algoritma bilgisine hakim olmanız gerekir.
Tanımlar
Bit: Bilginin en küçük birimidir. Varlık veya yokluğu ifade eder. Çoğunlukla varlık için 1, yokluk için 0 tercih edilir. Kullanıldığı bağlama göre ifade ediliş biçimi değişir. Örneğin; elektronikte varlık +12V, +5V, +3.3V gibi değerlerle ifade edilirken; yokluk 0V ifadesi ile edilir. 1
İkili sistem: Rakamları 0 ve 1 den oluşan bir sayı sistemidir.
Anlamlı bit ve anlamsız bit: Herhangi bir ikili sayıda (veya genel olarak herhangi bir sistemdeki herhangi bir sayıda) soldaki rakamlar sağdaki rakamlara göre daha fazla anlamlıdır. Bunlara sayıların basamakları denir. İkili sistemde en solda bulunan basamağa en anlamlı bit (MSB = most significant bit), en sağda bulunan basamağa ise en anlamsız bit denir (LSB = least significant bit). 2
İlham Kaynağı
Eğer toplama işlemini işlemciye tanımlatabilirsek; çıkarma işlemini, bölme ve çarpma işlemini tanımlayabiliriz.
Not: Ondalıklı sayılar işlemcilerin FPU adı verilen bir komponentinde işleme tabi olur. Yazının basitliği açısından, yazı FPU’yu kapsamayacaktır. Sadece ondalıklı sayıların da 1 ile 0 ile ifade edilebildiğini gösterip asıl konumuza devam edeceğiz. 3
Not 2: Toplama ve çıkarma çoğu işlemci için benzerdir. Ancak çarpma ve bölme için kullanılan algoritma işlemcilere özgüdür.
Rasyonel sayıların ikili sistemde ifadesi
İşlemci için tam sayı veya ondalıklı sayı gibi bir kavram ortada yoktur. Her şey sadece 1 ve 0 ile ifade edilir. Doğal sayıları ikili sisteme çevirmek kolaydır. Ancak işler negatif ve ondalıklı sayılara geldiğinde biraz karmaşıklaşıyor. İlk olarak doğal sayılarla başlayacağız sonrasında negatif sayıları ve ondalık sayıları ikili sistemdeki ifadesine geçeceğiz.
Doğal sayıların ikili sistemde ifadesi
Sayıyı 0 olana sürekli 2’ye bölerek kalan kısımları sondan başa doğru yazarak ikili sisteme çeviririz.
1
2
3
4
5
6
7
8
43 / 2 = 21 -> Kalan = 1
21 / 2 = 10 -> Kalan = 1
10 / 2 = 5 -> Kalan = 0
5 / 2 = 2 -> Kalan = 1
2 / 2 = 1 -> Kalan = 0
1 / 2 = 0 -> Kalan = 1
43 sayısının ikili sistemdeki karşılığı: 101011
IEEE 754 (Kayan noktalı sayıların ikili sistemde ifade edilmesinin standartı)
Bu standart iki duyarlılık seviyesine ayrılır:
- Tek Duyarlıklı (Single-Precision / float): 32-bit kullanılarak temsil edilir.
- Çift Duyarlıklı (Double-Precision / double): 64-bit kullanılarak temsil edilir.
Her iki format için sayıların en anlamlı biti işaret biti olarak adlandırılır. İşaret biti 1 ise sayı negatif, 0 ise sayı pozitiftir. Sonraki en anlamlı 8 bit (tek duyarlıklı) ya da 11 bit (çift duyarlıklı) exponent olarak adlandırılır. Geriye kalan 23 bit (tek duyarlıklı) ya da 52 bit (çift duyarlıklı) mantissa olarak adlandırılır.
Antrparantez: IEEE (Institute of Electrical and Electronics Engineers), elektrik, elektronik, bilgisayar, otomasyon, telekomünikasyon ve diğer birçok alanda mühendislik teori ve uygulamalarının gelişimi için çalışan, kâr amacı olmayan, dünyanın önde gelen teknik organizasyonudur. 4
Çevirme işlemi (1. adım)
x.y bir ondalık sayı olsun. Burada x tam kısım, y ondalık kısım olarak adlandırılır. Öncelikle tam kısmı yukarıda gösterdiğim gibi ikili sisteme çevireceğiz. Sonrasında ondalık kısmı çevirmemiz gerekiyor. Bunu 1 sayısına ulaşana kadar ondalık kısmı sürekli 2 ile çarparak sadece tam kısımlarını almamız gerekiyor.
1
2
3
4
5
6
7
8
9
10
11
43.25 sayısı için;
Bu sayı 43.25 = 43 + 0.25 şeklinde ifade edilir.
0.25 * 2 = 0.5 -> Tam kısım = 0
0.5 * 2 = 1 -> Tam kısım = 1
1. Tam kısım: 101011 (43)
2. Ondalık kısım: 01 (0.25)
olarak iki kısıma ayrılır.
Eğer bu çarpmalar sonucunda 1’e asla ulaşamıyorsak mantissa kısmını 23 (tek duyarlıklı) veya 52 (çift duyarlıklı) yapacak şekilde alırız. İşte bu da yuvarlama hatası (rounding error) doğurur. Sayılarda ufak bir hata payı oluşacaktır. Bu C kodunu printf("%f",43.185F); çalıştırırsanız 43.185001 değeri ile karşılacaksınız. Çünkü 43.185 girseniz de bu hatadan kaynaklı o sayı aslında 43.185001373291015625 şeklindedir. Bu yuvarlama hatasından dolayı meyadana gelir. Büyük “F” nin manası bu sayının tek duyarlıklı olduğunu ifade eder. “F” ibaresi belirtmeden deneseydik başarılı olurduk çünkü çift duyarlıklı sistemin kapsamı daha geniştir.
Not: C kütüphanesi için varsayılan davranış değiştirilmezse ondalık sayılar virgülden sonra 6 basamağa kadar ekrana yazılır. 5
Çevirme işlemi (2. adım)
Elde ettiğimiz iki değeri birleştirelim 101011.01 şeklinde olacaktır. Şimdi virgülü 1’in sağında gelecek şekilde 5 basamak sola kaydıralım. Sayımız sonunda 1.0101101 * $2^5$ şekline gelecektir. Sayımızı 5 basamak sola kaydırdığımız için Buradaki 2’nin üssüne tek duyarlıklı için 127, çift duyarlıklı için 1023 eklenir. Çıkan sonuç tekrardan ikili sisteme çevrilir ve bu kısıma exponent kısım denir.
1
2
3
Exponent: 5 + 127 = 132
Exponent kısım: 10000100
Çevirme işlemi (3. adım)
Virgül kaydırdığımız sayımızın virgülden sonraki kısmı (0101101) mantissa olarak adlandırılır ve burayı 23 (tek duyarlıklı) veya 52 (çift duyarlıklı) bite tamamlamamız gerekir. Bu yüzden 0101101’in sağına toplam 23 bit olacak şekilde 0 ekleriz.
1
2
3
4
5
6
7
8
9
43.25 sayısını IEEE 754 standartına göre tek duyarlıklı (32-bit) olacak şekilde ikili sistemde ifadesi
İşaret biti (1 bit): 0
Exponent kısmı (8 bit): 10000100
Mantissa kısmı (23 bit): 01011010000000000000000
43.25 -> 0 10000100 01011010000000000000000
olacaktır.
Negatif doğal sayıların ikili sistemde ifadesi
Negatif sayıları göstermek için ilgili sayının ikili sistemdeki karşılığının ikiye tümleyeni (two’s complement) alınır. Ancak bunun yapılabilmesi için bit sayısını 8,16,32 veya 64’e tamamlarız. Bunu bir örnek üzerinde gösterelim.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
-456 sayısının ikili sistemde ifadesi
Öncelikle 456 sayısını ikili sisteme çevirmeliyiz.
456 -> 111001000 şeklinde olur. Göreceğiniz gibi bu 9 bittir. Yani bu sayıyı 16,32 veya 64 bite tamamlayabiliriz. Burada en yakın olan 16'dır o yüzden bizde 16'ya tamamlayalım. Bu yapmak için toplam bit sayısı 16 olacak şekilde sayının soluna 0 ekleyelim.
456 -> 0000000111001000 olacaktır.
Şimdi bu ifadenin bire göre tümleyenini alacağız. Bunu yapmak için 1 yerine 0, 0 yerine 1 yazalım.
456 sayısının bire göre tümleyeni (one's complement): 1111111000110111
Son olarak bire göre tümleyinin üzerine 1 ekleyelim. Bu ifade -456 sayısının ta kendisidir.
-456 (456 sayısının ikiye göre tümleyeni) : 1111111000111000
bu işlemin tersi de mümkündür. Negatif bir sayının bire göre tümleyeninin üzerine 1 eklersek sayının pozitif halini buluruz.
Not: Binary sayılarda toplama işlemini ilerde anlatacağım.
Yukarıda görebileceğiniz gibi iki tür tümleyen şekli gösterdim. Peki biz neden sayıların negatifini alırken bire göre tümleyeni kullanmıyoruz? Bunun ikiye göre tümleyene göre farkı nedir onu gösterelim.
Aslında bunun en önemli sebebi bire göre tümleyen sisteminde 0 ve -0 sayıları ayrı tanımlıdır. Yani iki adet sıfır sayısı bulunur. Bu da aritmetikte yeri olmayan bir şeydir.
1
2
3
4
5
6
7
8
Çift sıfır sorunu
0 sayısının ikili sistemde ifadesi yine 0 olacaktır. Bunu en yakın 8 bite tamamlayalım.
00000000 şeklinde olur. Bunun bire göre tümleyeni 11111111 şeklinde olacaktır.
Eğer negatif sayıları bire göre tümleyenine göre gösterseydik iki adet sıfır olacaktı (0 ve -0). Ancak ikiye göre tümleyen esas alındığından bire göre tümleyeninin üstüne 1 eklenir. Bu da taşma (overflow) meydana getirir bunun sonucunda ifade tekrardan 00000000 şeklinde olur.
Nihayet gerekli tanımları ve çevirme aşamalarından sonra en önemli kısma geçebiliriz.
İkili sayılarda (Tam Sayılar için) toplama işlemi
Burada işlemcilerin yani ALU’nun nasıl toplama işlemi yaptığı ve insanların nasıl toplama işlemi yaptığını anlatacağım. İlk olarak insanların nasıl yaptığını anlatalım.
İnsanların toplaması
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
Öncelikle binary aritmetiğini anlamamız gerekir. Bunu anlamanız için 0 dan 10'a kadar olan sayıları göstereceğim.
0 = 0
1 = 1
2 = 10
3 = 11
4 = 100
5 = 101
6 = 110
7 = 111
8 = 1000
9 = 1001
10 = 1010
Temel aritmetiği umuyorum anlamışsınızdır.
Şimdi insanların nasıl toplama işlemini yaptığını gösterelim. Aynen normal toplama yapar gibi sağdan başlarız. Doğal olarak en sağdan başladığımız için elde sıfır olur.
Elde sıfırken;
0 + 0 = 0 ve eldeyi 0 yap,
0 + 1 = 1 ve eldeyi 0 yap,
1 + 0 = 1 ve eldeyi 0 yap,
1 + 1 = 0 ve eldeyi 1 yap.
Elde birken;
0 + 0 = 1 ve eldeyi 0 yap,
0 + 1 = 0 ve eldeyi 1 yap,
1 + 0 = 0 ve eldeyi 1 yap,
1 + 1 = 1 ve eldeyi 1 yap.
şimdi bunlara göre aşağıdaki işlemin sonucunu artık bulabiliriz.
00110101
01101101
+
----------------
10100010
ALU’nun toplaması
Not: ALU aritmetik ve lojik işlemleri gerçekleştiren işlemci komponentidir. Control unit ile kullanıcı istediği register ve talimat ile dört işlemleri ALU yardımıyla gerçekleştirebilir.
Not 2: Register (yazmaç) içerisinde sayıları tutabileceğimiz bellek ve önbelleğe göre kat ve kat daha hızlı bir işlemci komponentidir.
İşlemciler bu toplama işlemini full adder ve half adderleri kullanarak yaparlar.
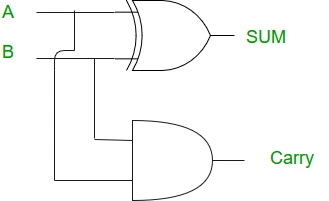
Half Adder
İki girişi ve iki çıkışı olan devredir. Girişleri sırasıyla A ve B, çıkışları sırasıyla toplam ve elde olarak ayrılır.
Toplam (SUM) çıkışı: A ⊻ B Elde (CARRY) çıkışı: A ∧ B
DOĞRULUK TABLOSU
| GİRİŞ A | GİRİŞ B | ÇIKIŞ TOPLAM (SUM) | ÇIKIŞ ELDE (CARRY) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
şeklindedir.
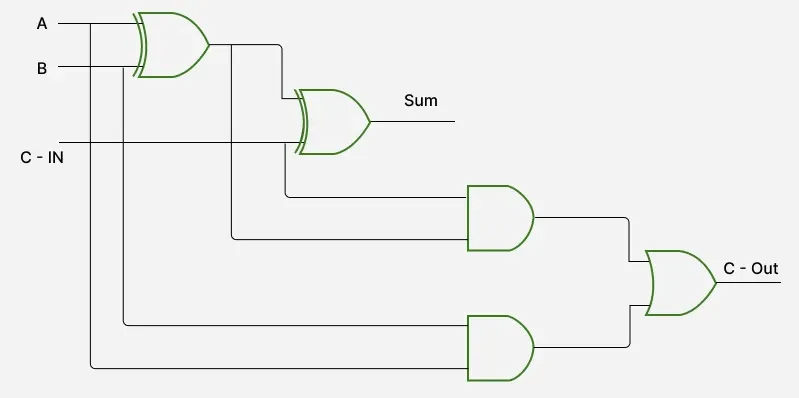
Full Adder
Üç girişi ve iki çıkışı olan devredir. Girişleri sırasıyla A,B ve elde; çıkışları toplam ve elde olarak ayrılır.
Toplam (SUM) çıkışı: (A ⊻ B) ⊻ elde (giriş) ELDE (CARRY) çıkışı: A ∧ B ∨ elde (giriş) ∧ (A ⊻ B)
DOĞRULUK TABLOSU
| GİRİŞ A | GİRİŞ B | GİRİŞ ELDE | ÇIKIŞ TOPLAM (SUM) | ÇIKIŞ ELDE (CARRY) |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
şeklindedir.
Farkedeceğiniz üzere half adder ve full adder devreleri birbirlerine benzerler ancak full adder ekstra olarak elde girişi de sağlar. İşlemcilerde 1-bitli sayıların toplama işlemini yapabilen iki devre tasarımını verdik. Sıra artık çok bitli sayılarda (8,16,32,64) bunların devre tasarımını yapabilmek artık çok kolay. Çünkü elimizde halihazırda olan full adder devrelerini birbirlerine bağlayarak istediğimiz bitte sayıyı toplayabiliriz. 8-bitlik sayılar için 8 adet, 16-bitlik sayılar için 16 adet, 32-bit için 32 adet, 64-bit için 64 adet yeterli olacaktır. Lakin ben anlatımı yaparken 8-bitlik sayılar üzerinden göstereceğim.
Şu örneğe geri dönelim:
1
2
3
4
5
00110101 = A
01101101 = B
+
----------------
10100010
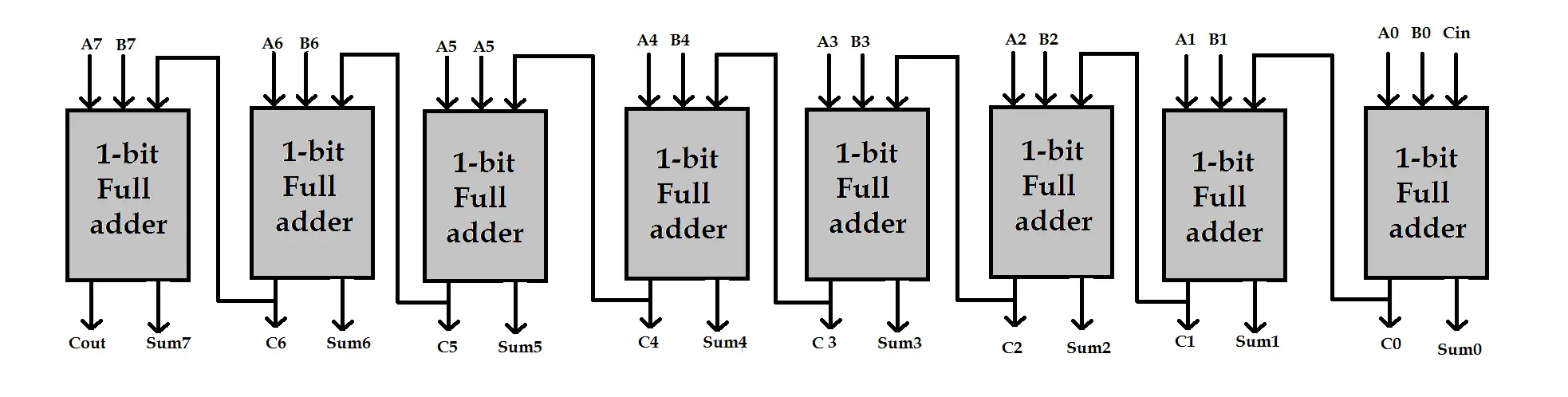
burada A0,A1,A2,…,A7 girişleri için A0 en anlamsız biti temsil ederken A8 en anlamlı biti temsil eder. Aynısı B0,B1,B2,…,B7 için de geçerlidir. Cin girişi, giriş eldesidir (INPUT CARRY). Cout çıkışı, çıkış eldesidir (OUTPUT CARRY).
Nihayet işlemcilerin içinde bulunan ALU komponentinin nasıl toplama işlemi yaptığını anladık.
Overflow: Biraz yukarıda bahsettiğim gibi 11111111 + 00000001 işlemini yaparsak toplama sonucunun 00000000 olacağını söylemiştim. Bunun sebebi bu devredir. Ancak Cout çıkışı 1 değerini alacaktır. Bu da ancak ve ancak overflow durumunda 1 değerini alır.
İkili sayılarda (Tam Sayılar için) çıkarma işlemi
1
2
3
A - B = A + (-B)
yukarıdaki ifade aşikardır. Dolayısıyla ALU, iki sayının farkını bulurken ikinci sayının negatifini alıp bu iki sayıyı toplayacaktır.
İkili sayılarda (Doğal Sayılar için) çarpma işlemi
Bilgi: İki adet A bitlik sayının çarpımı 2A bittir.
Bilgi 2: Bir sayıyı iki ile çarpmak demek sayıyı 1 bit sola kaydırmak demektir. Bu önermenin tam tersi de geçerlidir.
Kaydır-ve-ekle algoritması
Bunu örnekleyerek anlatacağım. Hem akış şemasında hem de sözde kodda 9x12 işlemini yapacağız.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
A = 0 (Her algoritma için aynı, bir nevi döngü için kullanılan değişken)
B = 9 -> 00001001
Q = 12 -> 00001100
C = Q'nun en anlamsız biti (LSB)
N = 8 (B ve Q'nun bit sayısı)
ALGORİTMA BAŞLANGICI
İŞARET H
EĞER C = 1 ise:
A = A + B
A ve Q değerlerini birleştirerek (yan yana hali) 1 bit sağa kaydır
N = N - 1
EĞER N = 0 DEĞİLSE:
GİT İŞARET H
ALGORİTMA SONU
Algoritma bittikten sonra istediğimiz değer A VE Q değerlerinin birleştirilmiş halidir.
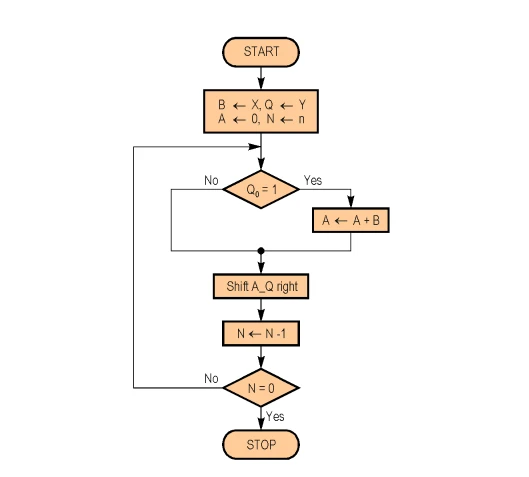
Not: İşaretli sayılar için çarpma işlemi booth algoritması ile olur. Onun sözde kod halini vermeyeceğim ama akış şemasını ekleyeceğim.
Booth algoritması
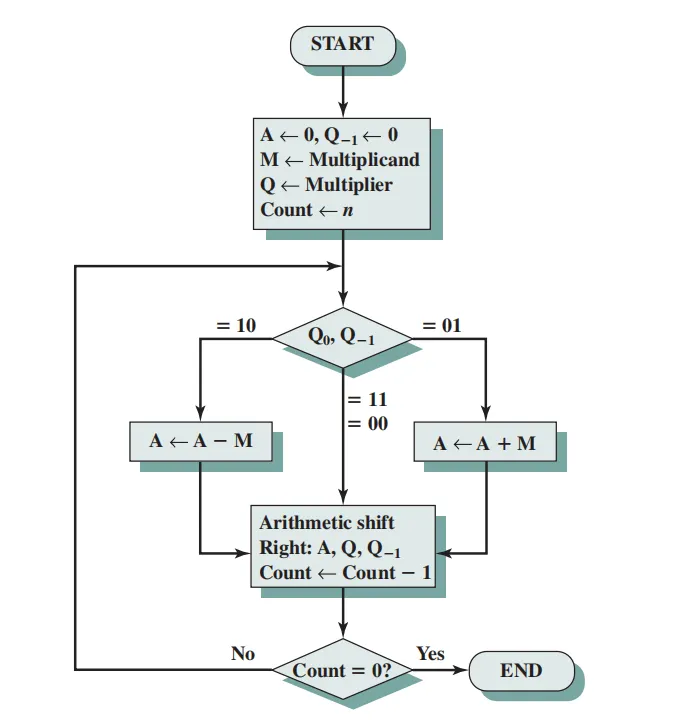
İkili sayılarda (Doğal Sayılar için) bölme işlemi
Bilgi: 2A bitlik sayının bölümünde; bölen, bölümün sonucu ve kalanı A bittir.
Bu algoritmaya tekrarlı çıkarma da denebilir.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
R = BÖLÜNEN (Herhangi bir pozitif sayı)
D = BÖLEN
Q = 0
ALGORİTMA BAŞLANGICI
R >= D iken:
R = R - D
Q = Q + 1
ALGORİTMA BİTİŞİ
Algoritma sonunda R kalanı, Q bölümü ifade eder.
Bitiş
Yazının başında da belirttiğim gibi çarpma ve bölme için kullanılan algoritmalar çok çeşitlidir. Bu nedenle kullanılan algoritma donanıma özgüdür. Bu yazıda gösterdiğim çarpma ve bölme için olan algoritmaları en basit olacak şekilde seçtim.
Bu yazıları yazma sebebim sizin bu algoritmaları ezberlemeniz veya sayılar ikili sisteme çevirmeyi öğretmek değildir. Asıl amacım size kendi kendinize öğrenebilme yeteneğini kazandırmaktır. Sorunları kendi kendinize çözebilme yeteneğini kazandırmaktır.
İleri Okuma
Division algorithm - Wikipedia
Kaynakça
[1]: https://tr.wikipedia.org/wiki/Bit_(bili%C5%9Fim)
[2]: https://en.wikipedia.org/wiki/Bit_numbering
[3]: https://en.wikipedia.org/wiki/Floating-point_unit#cite_ref-1
[4]: https://www.ieee.org/about-ieee
[5]: https://en.cppreference.com/w/c/io/fprintf.html
