Otomata Teorisi Nedir?
Otomata teorisinin temellerini, sonlu otomatları, düzenli dilleri, yığıtlı otomasyonları ve Chomsky Hiyerarşisi’ni inceleyen kapsamlı bir giriş yazısı.
Otomata Teorisine Giriş
Bu yazıda bilgisayar bilimlerinde önemli olan otomat teorisini inceleyeceğiz.
Otomata Teorisi nedir?
Otomata Teorisi , Hesaplama Kuramı’nın bir alt dalıdır. Bilgisiayar bilimleri ve matematikte makinelerin hesaplamalarıyla ilgili sınırlamalarını ve hangi hesaplamaları yapabildiğini inceleyen bir alandır.
Otomata teorisi nerelerde kullanılır?
1- Dijital devrelerin davranışını tasarlamak ve kontrol etmek için kullanılan yazılımlar
2- Tipik bir derleyicinin sözlük analizörünü mantıksal birimlere ayıran derleyici bileşeni
3- Büyük metinleri taramak için geliştirilen yazılımlar
4- Sonlu sayıda farklı duruma sahip sistemleri doğrulamak için kullanılan yazılımlar
Otomata Teorisinin Temel Kavramları
Bu bölümde otomat teorisini en çok etkileyen en önemli terimlerin tanımlarını inceleyeceğiz.
Alfabe
Sonlu ve boş olmayan semboller kümesidir ve göstermek için Σ (sigma) sembolü kullanılır. Yaygın olarak kullanılan bazı alfabeler şunlardır:
-Σ = {0, 1} → İkili (binary) alfabe -Σ = {a, b, …, z} → Tüm küçük harflerden oluşan alfabe -Tüm ASCII karakterleri kümesi veya yalnızca yazdırılabilir ASCII karakterlerinin kümesi
Dizgiler
Bir alfabeden seçilmiş sonlu sayıda sembolden oluşan bir sıralamadır.
Örneğin 011001, {0,1} ikili alfabesinden alınmış bir dizgidir. 111 de aynı alfabeden alınmış bir başka dizgidir.
Bir Alfabede Üs Gösterimi
Eğer Σ bir alfabe ise, bu alfabeden oluşan belirli uzunluğa sahip dizgiler kümesi üs notasyonu kullanılarak ifade edilebilir.
Σ⁽ᵏ⁾ ifadesi, Σ alfabesindenki sembollerden oluşan ve uzunluğu tam olarak k olan tüm dizgilerin kümesini tanımlar.
Diller
Bir dil, tamamı belirli bir kümesinden seçilmiş dizgilerden oluşan bir kümedir.
Eğer Σ bir alfabe ve L ⊆ Σ* ise, o zaman L, Σ alfabesi üzerinde tanımlı bir dildir.
Sonlu Durum Makineleri
Sonlu durum makineleri, düzenli dilleri tanımlamak için kullanılan en temel soyut makinelerden biridir. Bu makineler belirli girdilere göre bir durumdan başka bir duruma geçerek çalışırlar.
Sonlu otomatlar iki ana sınıfta incelenir:
Deterministik Sonlu Otomatlar
Sonlu otomatlar tanımında yazdığı üzere girdiye göre bir durumdan başka bir duruma geçerek çalışırç Deterministik sonlu otomatlar mevcut durumdan yalnızca bir duruma geçiş yapar. Bir deterministik sonlu otomat aşağıdaki bileşenlerden oluşur:
- Sonlu bir durum kümesi, genellikle Q ile gösterilir.
- Sonlu bir giriş sembolleri kümesi, genellikle Σ ile gösterilir.
- Geçiş fonksiyonu (δ) — bir durumu ve bir giriş sembolünü argüman olarak alır ve bir yeni durum döndürür.
- Başlangıç durumu Q kümesindeki durumlardan biridir ve genellikle q₀ ile gösterilir.
- Kabul eden (final) durumlar kümesi, genellikle F ile gösterilir. F, Q’nun bir alt kümesidir.
A, otomatın adı olmak üzere A=(Q,Σ,δ,q0,F) şeklinde gösterilir.
Bir deterministik sonlu otomat girdileri işleme sürecine alır. İşleme sonucu ulaşılan son durum bu kümedeyse girdiyi kabul eder. Bir determinisitik sonlu otomatın dili de kabul ettiği tüm dizileri kümesi olur.
Belirsiz (Deterministik Olmayan) Sonlu Otomatlar
Belirsiz sonlu otomatlar da deterministik sonlu ototmatlar gibi sonlu sayıda durumdan oluşur, sonlu sayıda giriş sembolüne sahiptir, başlangıç durumu, kabul durumu kümesi vardır, ayrıca geçiş fonksiyonuna da sahiptir.
İkisi arasındaki farkı da geçiş fonksiyonu türü belirler. Belirsiz sonlıu otomatlarda sonuç sıfır, bir veya birden fazla oluşan bir küme döndürür. Bu aynı anda birden fazla durumda olma yetisi genellikle girdi hakkında bir şeyi tahmin etme yeteneği olarak ifade edilir.
Düzenli Diller
Düzenli diller olarak bilinen dil sınıfı dört farklı şekilde tanımlanabilir. Bunlardan biri Deterministik sonlu otomat tarafından kabul edilen diller, diğeri ise belirsiz sonlu otomat tarafından kabul edilen diller şeklinde yapılan tanımdır.
Her dil düzenli olmadığı için belirli pumping lemma gibi teknikler kullanılarak dilin düzenli olup olmadığı anlaşılır.
Pushdown Automata
Pushdown Automata’yı anlatmadan önce bazı kavramları incelememiz gerekir.
Bağlamdan Bağımsız Gramer
Bağlamdan bağımsız gramer dört bileşenli bir yapıdır ve şu şekilde tanımlanır:
G = (V,T,P,S) V: Değişkenler kümesi T: Alfabe (terminal semboller) P: Üretim kuralları kümesi S ∈ V: Başlangıç sembolüdür
Bağlamdan bağımsız gramer bize bir dili tanımlamanın yolunu verir. Hangi dizgiler o diler aittir, hangileri değildir sorusuna cevap verir.
Bağlamdan Bağımsız Dil
Bir dili oluşturan dizgiler V,T,P,S bileşenleriyle tanımlanabiliyorsa, yani o dili tanımlayan bir bağlamdan bağımsız bir gramer varsa veya tanımlyan yığıtlı otomasyon (pushdown automaton) varsa o dil bağlamdan bağımsız dildir.
V = Kuralların içindeki değişkenleri tanımlar. Bunlar dilin yapısal bölümleridir. T = Gerçek giriş sembolleridir. Yani dilin kelimeleri, karakterleri, sembolleri. P = Türetim kurallarıdır. Hangi değişkenin, hangi sembollere veya diğer değişkenlere dönüşebileceğini söyler. S = Türetimin başladığı yerdir. Yani dilin tanımının başlangıç noktası.
Yığıtlı Otomasyon
Bağlamdan bağımsız dillerin, onları tanımlayan özel bir otomat türü vardır. Bu otomat, yığıtlı otomat olarak adlandırılır. Yığıtlı otomat, ε-geçişlerine izin veren belirsiz sonlu otomatın bir uzantısıdır.
Düzenli dillerin tanımlanmasında kullanılan yöntemlerden biri olan bu yapı, üzerine bir yığıt eklenerek güçlendirilmiştir. Yığıtın varlığı, sonlu otomatların aksine, yığıtlı otomasyonun sınırsız miktarda bilgiyi “hatırlamasını” sağlar. Ancak bu genel amaçlı bir bilgisayar gibi değildir. Çünkü yığıtlı otomasyon yalnızca son giren, ilk çıkar (LIFO) şeklinde yığıt erişimi yapabilir.
Deterministik Sonlu Otomasyon vs. Yığıtlı Otomasyon
- DSO sabit bellek kullanır, yığıtlı otomasyon buna ek olarak yığıt kullanır
- DSO düzenli dilleri tanır, yığıtlı otomasyon bağlamdan bağımsız dilleri tanır
- Yığıtlı otomasyon yığıt sayesinde geriye bakma yeteneğine sahiptir,DSO için böyle durum söz konusu değildir.
Chomsky Hiyerarşisi
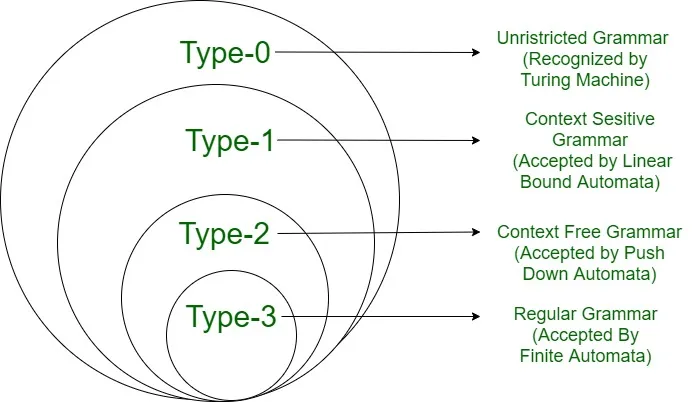
Noam Chomsky tarafından 1956’da ortaya atılmıştır. Amacı farklı gramer türlerinin ne kadar güçlü olduğunu göstermektir.
Tip-0: Kısıtlanmamış Gramer
Tip-0 gramerler tüm biçimsel gramerleri kapsar. Bu gramerlerin tanımlandığı diller Turing makineleri tarafından tanınır.
Tip-1: Bağlama Duyarlı Gramer
Bu gramerler bağlama duyarlı dilleri üretir. Bu diller lineer sınırlı otomat tarafından tanınır.
Tip-2: Bağlamdan Bağımsız Gramer
Bu gramerler bağlamdan bağımsız dilleri üretir. Tanımlanan diller yığıtlı otomat tarafından tanınır.
Tip-3: Düzenli Gramer
Bu gramerler düzenli dilleri üreti. Sonlu otomatlar tarafından tanınabilir. Bu hiyerarşideki en kısıtlı ancak en verimli sınıftır.
Sonuç
Sonuç olarak otomata teorisi bilgisayar bilimlerinin temel yapı taşlarından biridir. Çünkü dillerin nasıl tanındığı, yazılım sistemlerinin çalışma şekli ve algoritmaların neler yapıp yapamayacağını anlamamıza yardımcı olur. Bir derleyicinin programı analiz edebilmesi veya bir sistemin doğru girişleri kabul edip hatalı olanları reddetmesi arkada bir otomat sisteminin çalıştığının göstergesidir.
Düzenli ifadeler,derleyiciler,doğal dil işlemei,ağ protokolleri ve oyun motorları gibi pek çok sistem içinde çalışırak düzgün bir şekilde işlemelerinde önemli bir yer tutar.
Kaynakça
- Introduction to Automata Theory, Languages and Computation
- https://www.geeksforgeeks.org/theory-of-computation/
- https://www.univ-orleans.fr/lifo/Members/Mirian.Halfeld/Cours/TLComp/TLComp-introTL.pdf
- https://en.wikipedia.org/wiki/Automata_theory
- https://cs.stanford.edu/people/eroberts/courses/soco/projects/2004-05/automata-theory/basics.html
