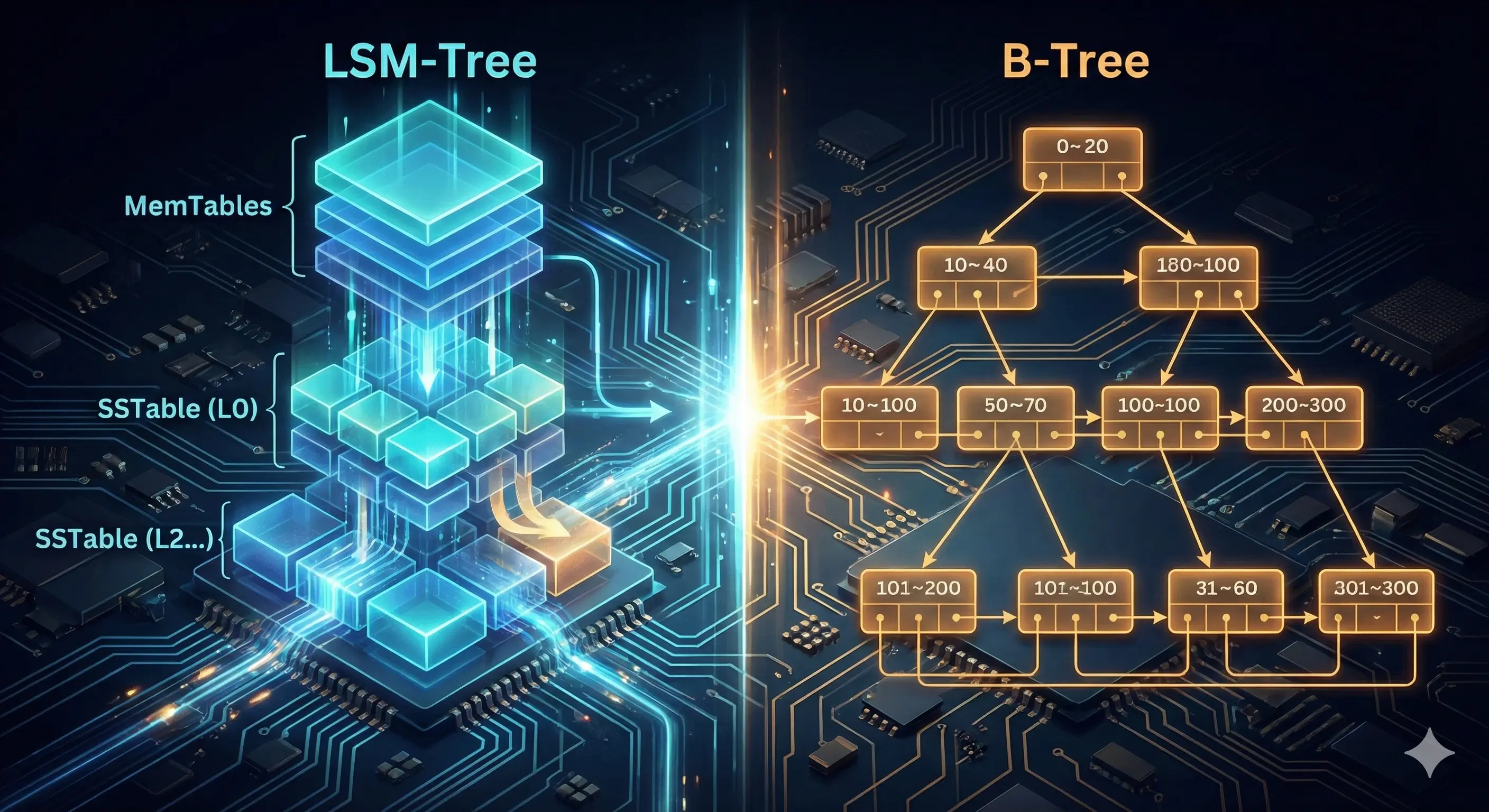
Log-Structured mı, B-Tree mi? Verinizi Saklamanın İki Farklı Felsefesi
Veri tabanlarının kalbi olan depolama motorlarını, Log-Structured Merge-Trees (LSM) ve B-Trees arasındaki farkları, 'Data-Intensive' uygulamalar perspektifinden ve Martin Kleppmann'ın DDIA kitabı ışığında inceliyoruz.
No Silver Bullet
Yazılım mühendisliğinde gümüş kurşun yoktur.
Herkese selamlar! Uzun bir aradan sonra, şu sıralar üzerinde yoğun mesai harcadığım Martin Kleppmann’ın “Designing Data-Intensive Applications” (DDIA) kitabı üzerinden dilimizde yeterince kaynağı bulunmayan bir konuyu anlatacağım. Bugün merceğimizde, veri tabanlarının kalbi sayılan depolama motorları ve bu motorların temelini oluşturan iki dev yapı var: Log-Structured Merge-Trees (LSM-Trees) ve B-Trees.
Peki hangisi daha iyi? Kısa cevap: “duruma göre değişir”. Uzun cevap: “bu yazının konusu”.
Data-Intensive Nedir?
Temel olarak bir veri tabanından beklentimiz basittir: Ona bir veri verdiğimizde onu güvenle saklamalı (POST) ve istediğimizde bize geri vermelidir (GET). Muhtemelen çoğumuz kariyerimiz boyunca sıfırdan bir veri tabanı motoru inşa etmeyeceğiz; ancak sürekli olarak “Data-Intensive” (Veri Yoğun) uygulamalar geliştireceğiz.
Peki, bir uygulamaya ne zaman “Data-Intensive” diyoruz? Eğer uygulamanızın temel darboğazı (bottleneck) hesaplama gücü (CPU-intensive) değil de; verinin miktarı, karmaşıklığı veya değişim hızı ise, o uygulama artık “Data-Intensive” olarak sınıflandırılır. Yani sisteminiz artık I/O-bound (Giriş/Çıkış kısıtlı) hale gelmişse ve performansınızı belirleyen ana faktör disk veya ağ hızıysa, hoş geldiniz, artık veri yoğun bir dünyadasınız.
Veri tabanlarını genellikle SQL veya NoSQL (veya son dönemin popüler yönelimi NewSQL) olarak ayırsak da, asıl ayrım “kaputun altında” verinin nasıl depolandığında yatar. Günümüzde bu konuda iki temel yaklaşım hakimdir: LSM-Tree ve B-Tree.
OLTP Dünyasında Depolama ve İndeksleme
Konuya girmeden önce sahneyi kurmak lazım: OLTP (Online Transactional Processing). Bu sistemler, kullanıcıların veri tabanıyla sürekli etkileşime girdiği, çok sayıda küçük okuma ve yazma işleminin (transaction) anlık gerçekleştiği yerlerdir (günlük olarak SQLite, endüstriyel çözüm olarak PostgreSQL & MySQL). Bunun kardeşi olan OLAP (Online Analytical Processing) ise analiz odaklı veri tabanlarını tanımlamak için kullanılır (gündelik çözüm olarak DuckDB, büyük ölçekli olarak Google BigQuery & Amazon Redshift).
Endüstride hız her şeydir çünkü hız $∝$ paradır. Veri tabanının veriyi nasıl indekslediği, milisaniyeler seviyesindeki performans farkını belirleyen ana unsurdur. İndeksleme, kabaca veriye giden bir “kısayol” oluşturmaktır. Ancak her kısayolun bir maliyeti vardır çünkü 1 milyon fazladan indeksleme, kabaca 1 milyon fazladan anahtar demektir (ve bu da yazma hızını baltalar, bir trade-off yaratır). İşte LSM-Tree ve B-Tree arasındaki kadim savaş da tam bu noktada, “Yazma hızı mı, yoksa okuma hızı mı?” sorusuyla başlar.
Log-Structured Storage
Bu iki bash fonksiyonuna bakalım:
1
2
3
4
5
6
7
8
9
#!/bin/bash
db_set () {
echo "$1,$2" >> database
}
db_get () {
grep "^$1," database | sed -e "s/^$1,//" | tail -n 1
}
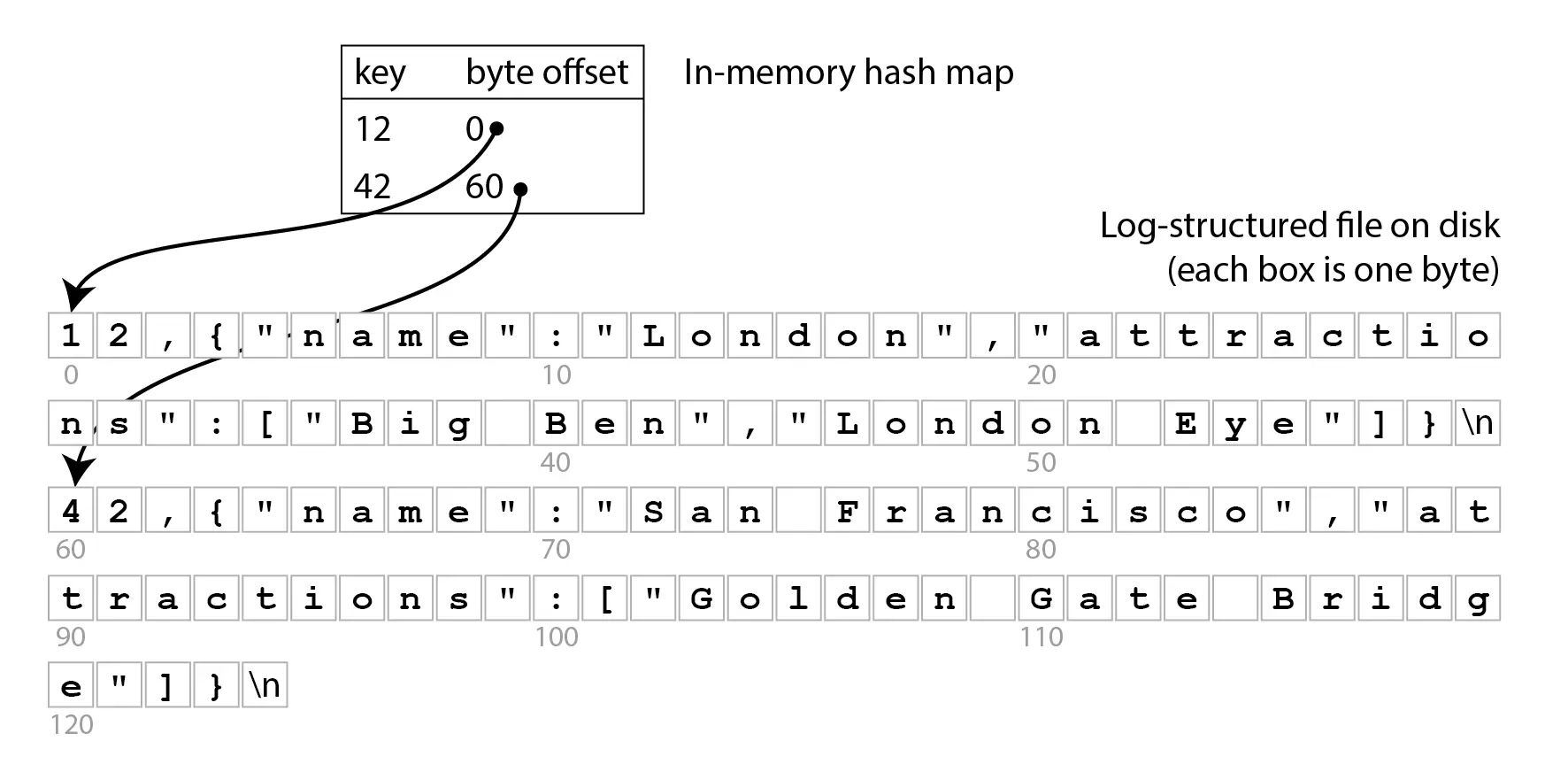
Bu iki işlev, anahtar-değer (key-value) çiftiyle çalışan basit bir veri tabanı oluşturur. db_set fonksiyonunu bir setter, db_get fonksiyonunu ise bir getter olarak düşünelim. Anahtar ve değer (neredeyse) istediğiniz her şey olabilir; örneğin, değerimiz bir JSON belgesi olabilir. Ardından db_get işlevini anahtarla çağırarak, o anahtarla ilişkili en son değeri arayabilir ve döndürebilirsiniz.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
$ db_set 12 '{"name":"London","attractions":["Big Ben","London Eye"]}'
$ db_set 42 '{"name":"San Francisco","attractions":["Golden Gate Bridge"]}'
$ db_get 42
{"name":"San Francisco","attractions":["Golden Gate Bridge"]}
$ db_set 42 '{"name":"San Francisco","attractions":["Exploratorium"]}'
$ db_get 42
{"name":"San Francisco","attractions":["Exploratorium"]}
$ cat database
12,{"name":"London","attractions":["Big Ben","London Eye"]}
42,{"name":"San Francisco","attractions":["Golden Gate Bridge"]}
42,{"name":"San Francisco","attractions":["Exploratorium"]}
Bu yapı dünyanın en basit veri tabanıdır ve veriler üst üste yığılarak ilerler. Yani bir anahtar için son değer nihai durumu belirtir ve öncekiler önemsizdir, cat çıktısında da görebiliyoruz. Bu yapının verdiği en büyük ödün ise devasa veri tabanlarındaki okuma zorluğudur.
Log-Structured Merge Trees (LSM-Trees)
Gerçek dünya uygulamalarında veriler genellikle bir hash fonksiyonundan geçirilir ve bazı durumlarda RAM’de verinin hash bilgisi tutulur. Hash, matematiksel olarak oluşturulan ve tek yönlü gidilebilen (tabii eğer güvenli bir matematiği varsa) bir özetleme aracıdır. Örneğin:
1
2
3
4
5
6
7
8
9
10
>>> hash
<built-in function hash>
>>> hash("data")
-1021977521653558605
>>> hash("data.")
-8687997014242317588
>>> hash("data")
-1021977521653558605
>>> hash("data.")
-8687997014242317588
Gördüğümüz üzere sadece ‘.’ eklememiz bile veriyi uçtan uca değiştirmekte, ancak aynı veri için aynı hash değeri oluşmaktadır.
LSM-Tree MemTable Yapısı
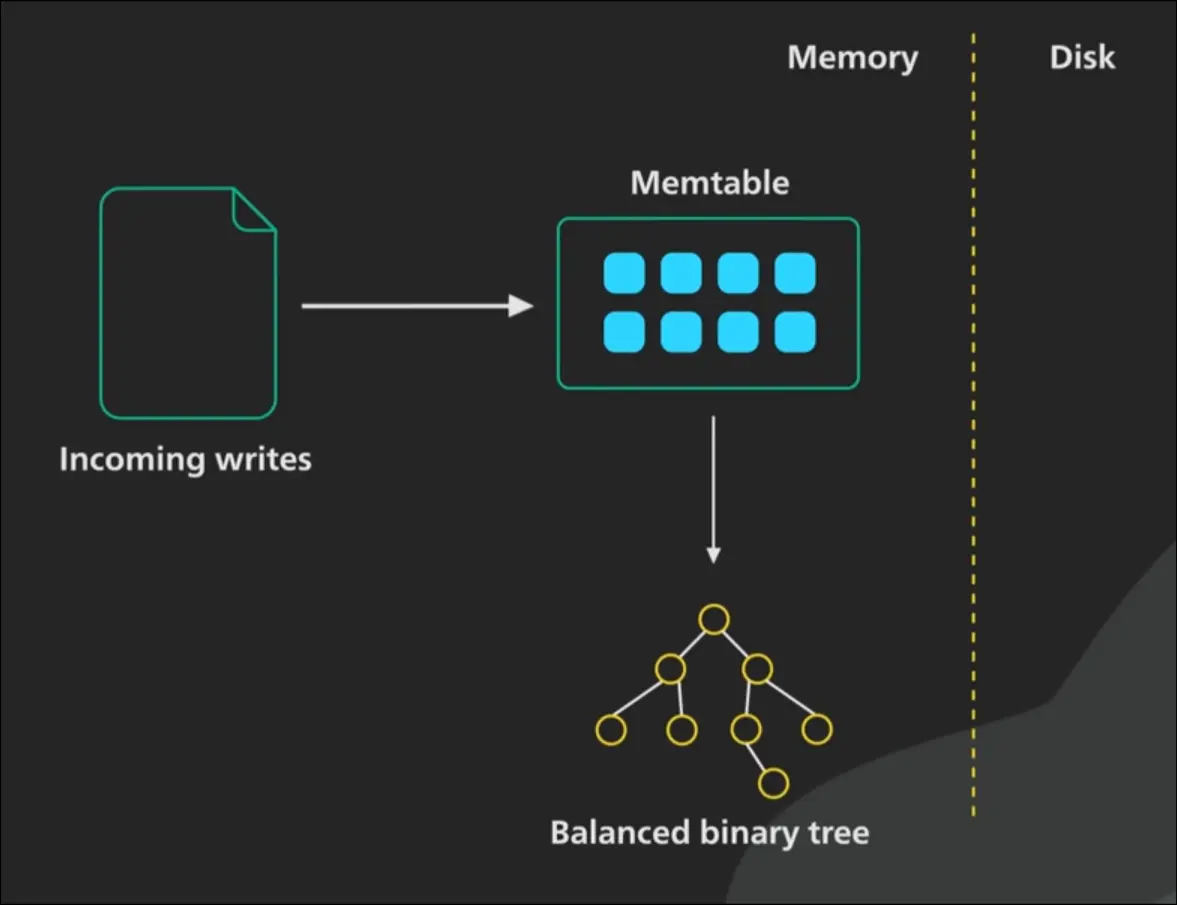
Yukarıda bir LSM-Tree’nin RAM (in-memory) kısmını görmekteyiz. Bu yapıya genel olarak MemTable veya C0 adı veriliyor. MemTable özünde bir balanced binary tree‘dir (dengeli ikili ağaç). Burada Red-Black veya AVL gibi ağaç veri yapıları tercih edilmektedir. Tabii ki genellikle hiçbir büyük veri tabanı saf bir ağaç kullanmaz, genellikle büyük optimizasyonlar yapar ve bunlara Skip List denir.
LSM-Tree’lerde Okuma ve Yazma Metotları
Peki RAM dolmaya başlayınca ne olur? Eğer ağaç bellekte veri tabanının belirlediği bir büyüklüğe ulaştığında, flush denilen işleme tabi tutulur. Flush, tamponda (buffer) tutulan verinin asıl işlem yerine gönderilmesi işlemidir ve veri buradan sonra Sorted String Table (SSTable) adını alır.
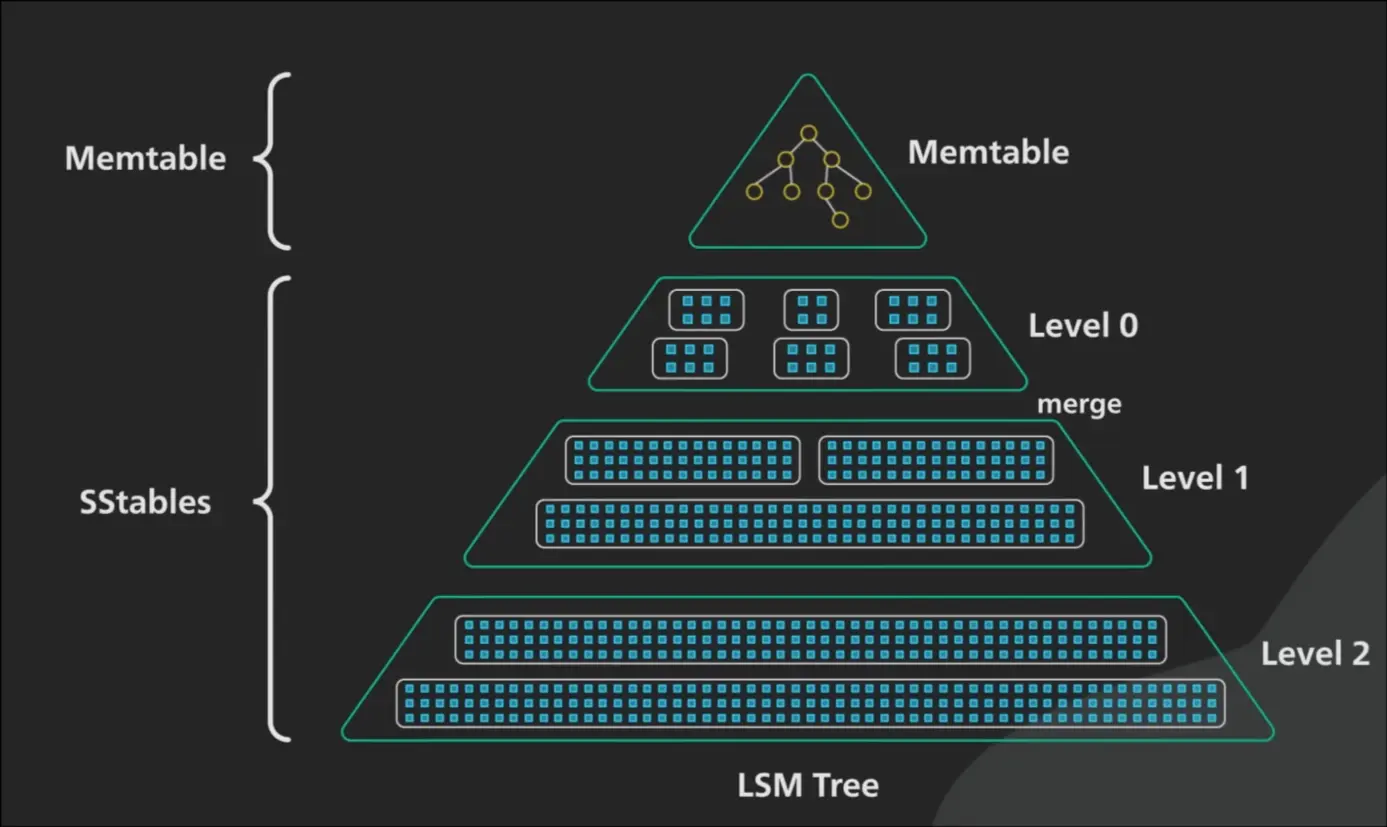
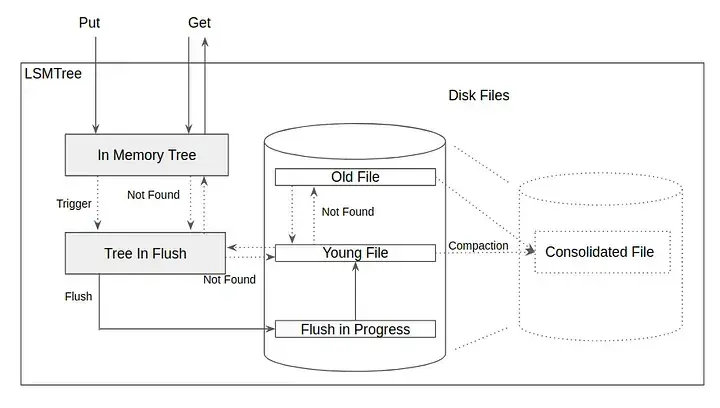Sorted String Table (SSTable) Yapısı - 1
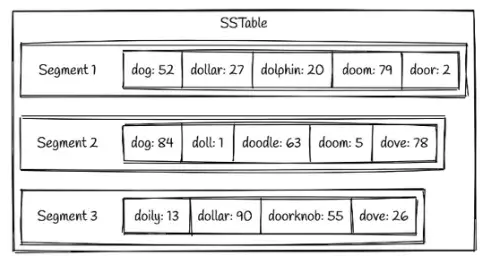Sorted String Table (SSTable) Yapısı - 2
Her tablo bir sonraki tablonun üstünde yer alır. Okuma mantığını ise LIFO (Last In First Out) gibi hayal edebiliriz; kronolojik olarak geriye gidilerek okuma yapılır ve bu da veri doğruluğunu garanti eder.
LSM Ağaçlarının 2 büyük “trade-off”u vardır:
- Okuma Yükü: Tabloda sadece değişiklikler yer aldığı için, eğer bir key (anahtar) o anki tabloda yoksa her seferinde bir önceki tabloya bakmamız gerekir. Baktığımızda büyük bir düzen söz konusu olsa da her tablo için ek bir okuma yükü oluşur ve sistem yavaşlayabilir.
- Disk Alanı: Tablolar kesinlikle immutable yani değiştirilemezdir ve her güncelleme işlemi için yeni kayıt açılır. Bu da yine düzen sağlar ancak disk alanını çok hızlı doldurur.
Peki ya silme yapılacaksa? Evet, alışık olmadığımız şekilde silme işlemi veriyi diskten silmiyor çünkü tablolar değiştirilemezdir. Bunun yerine Tombstone (mezar taşı) adı verilen silme kaydı tabloya eklenir. Yani sırasıyla verileri okurken tombstone var ise o veri silinmiş demektir, ancak fiziksel olarak diskte yer almaya devam eder (ta ki Compaction işlemi yapılana kadar).
LSM-Tree’lerin Optimizasyonu ve Yönetimi
Bu bölümde 4 temel soruya yanıt arayacağız:
- Elektrik giderse RAM’deki (MemTable) veriye ne olur?
- Binlerce dosya oluştu, aradığımı bulmak için hepsine mi bakacağım?
- Disk dolup taşmıyor mu?
Felaket Senaryosu: Elektrik Giderse Ne Olur? (WAL)
Veri bütünlüğünü sağlamak, veri tabanı dünyasının ve Data-Intensive uygulamaların en büyük ve en eski problemidir. Bir veri tabanı tasarımında ilk kural: “Veri asla doğrudan diske yazılmaz!”
Veri her zaman önce Write Ahead Log (WAL) denilen bir dosyaya yazılır. WAL, aslında her adımınızı not alan bir gözetmen gibidir. Örneğin veri tabanı 42 numaralı satırı taşıyacaksa oraya detaylı bir bilgi bırakmak zorunda:
“Ben 42. satırdaki ve x bloğunda olan y bilgisini, z numaralı bloğa taşıyorum”
Olası bir sorun durumunda veri tabanı bunu açıldığı anda okuyarak bütünlüğü kontrol eder.
Samanlıkta İğne Aramak: Bloom Filters
Okuma hızının yavaş olabileceğini (bir sürü dosyaya bakmak gerektiğini) söylemiştik. Burada devreye matematik giriyor.
Disk üzerinde yüzlerce SSTable segmenti oluştu. Aradığımız user_id: 123 hangi dosyada? Hepsini tek tek açıp bakmak inanılmaz bir I/O maliyetidir. İşte burada Bloom Filter denilen olasılıksal bir veri yapısı devreye girer.
Her veri noktası için 10 bit harcayıp (1 Megebaytın 800.000’de biri) bir dosyada olup olmadığına (daha doğrusu kesin olarak olmadığına) anında karar verebildiğimiz akıllıca bir takastır (trade-off) bu filtre. Her SSTable için bir bitmap tutuyoruz. Sisteme bir anahtar eklendiğinde:
- Anahtar, birkaç farklı hash fonksiyonundan geçirilir ve ortaya çıkan sayılar bit dizisindeki ilgili indekslere karşılık gelir.
- Bu indekslerdeki bitler
1yapılır. - Bir anahtarı ararken aynı hash fonksiyonlarını çalıştırırız. Eğer karşılık gelen bitlerden yalnızca biri bile
0ise, o anahtar o dosyada kesinlikle yoktur. - Eğer tüm bitler
1ise, anahtar o dosyada olabilir.
Kleppmann’ın bahsettiği üzere anahtar başına sadece 10 bitlik bir alan ayırırsanız, %1 gibi çok düşük bir hata payı elde edersiniz. Ayırdığınız her fazladan 5 bit, bu hata olasılığını on kat daha azaltır.
Merging & Compaction
Sürekli yeni SSTable’lar oluşturmak, bir süre sonra diski adeta bir “dosya çöplüğüne” çevirir. Bu sadece disk alanı israfı değil, aynı zamanda okuma yaparken bakmanız gereken dosya sayısının artması demektir. Bu sorunu çözmek için arka planda sürekli çalışan bir “temizlik ve düzenleme” süreci işletiriz: Compaction.
Bu süreç aslında bildiğimiz Merge Sort (Birleştirme Sıralaması) algoritması gibi çalışır. Arka plandaki işlemci, farklı zamanlarda oluşturulmuş SSTable dosyalarını yan yana koyar ve içlerindeki anahtarları sırayla okur.
Burada iki önemli işlem gerçekleşir:
- Güncellenmiş Verilerin Ayıklanması: Eğer aynı anahtar birden fazla dosyada varsa, sadece en güncel (en son yazılmış) olanı yeni dosyaya aktarır, eskilerini çöpe atarız.
- Tombstone (Silme İşlemi): Eğer bir veri silindiyse, onun için oluşturduğumuz “tombstone” kaydı, birleştirme sırasında eski verilerin tamamen yok edilmesini sağlar. Mezar taşı en eski segmente kadar ulaştığında o da artık sistemden atılabilir.
Bu işlem sırasında veri tabanı durmaz; sistem eski dosyaları kullanarak okuma isteklerine cevap vermeye devam eder. Birleştirme bittiğinde, yeni oluşturulan tertemiz ve tek parça SSTable dosyasına geçilir ve eski dosyalar silinir.
Burada iki teknik vardır:
- Size-tiered Compaction (Boyut Odaklı): Yeni ve küçük olan SSTable’lar zamanla kendilerinden daha büyük olan eski dosyalara katılır. Yazma hızının çok yüksek olduğu senaryolar için idealdir. Apache Cassandra bunu tercih eder.
- Leveled Compaction (Seviye Odaklı): Veriler sabit boyutlu parçalara bölünür ve L0, L1 gibi seviyelere ayrılır. Okuma işlemlerinde daha kararlıdır çünkü bakmanız gereken dosya sayısı çok daha azdır. L0 haricinde birbirini ezen bir anahtar bulunmaz. RocksDB ise bunu tercih eder.
Yine bir trade-off söz konusu.
LSM-Tree Compaction Süreci
LSM-Tree’ler, verinin daha az okunduğu, ağırlıklı olarak sürekli yeni verinin geldiği sistemlerin felsefesidir. Ancak verinin çoğunlukla okunmak için çağırıldığı bir dünyada LSM ağaçları inanılmaz bir bottleneck’e neden olur ve bu durumda ise 50 yıldır işletim sistemlerinin çekirdeğine taht kurmuş B-Tree’ler ortaya çıkar.
B-Trees
Duyurulduğu günden beri neredeyse tüm ilişkisel veri tabanlarında ve bir çok ilişkisel olmayan veri tabanında merkezde yer alan B-Tree’ler, LSM-Tree’lere göre oldukça yüksek okuma hızı sunuyor. Sanılanın aksine ‘B’ harfinin burada ne anlama geldiği hiçbir zaman açıklanmadı (Boeing? Balanced? Bayer?).
B-Tree’ler, klasik ikili arama araçlarından oldukça farklı bir yapıdadır. Daha önce gördüğümüz LSM ağaçları, veri tabanını değişken boyutlu segmentlere ayırır; bu segmentler genellikle birkaç Megabayt veya daha büyük boyutlardadır, bir kez yazılır ve daha sonra değiştirilemez. Buna karşılık, B-Tree’ler veri tabanını sabit boyutlu bloklara veya sayfalara ayırır ve bir sayfayı yerinde üzerine yazabilir. Bir sayfanın boyutu geleneksel olarak 4 KiB‘dir, ancak PostgreSQL artık 8 KiB ve MySQL varsayılan olarak 16 KiB kullanmaktadır.
Bu boyutların 4 KiB seçilmesi tesadüf değildir; donanım seviyesinde disk blokları ve işletim sistemi sanal bellek sayfaları (OS pages) genelde 4 KiB’dır. B-Tree donanımla aynı dili konuşur.
1
2
3
4
5
6
❯ free -h
total used free shared buff/cache available
Mem: 15Gi 7.1Gi 1.2Gi 210Mi 7.7Gi 8.4Gi
Swap: 23Gi 1.3Gi 22Gi
# Kapattığınız uygulamalar (ve nesneler) tamponda (buffer) bekletilir.
# Unutmayın "unused RAM is wasted RAM".
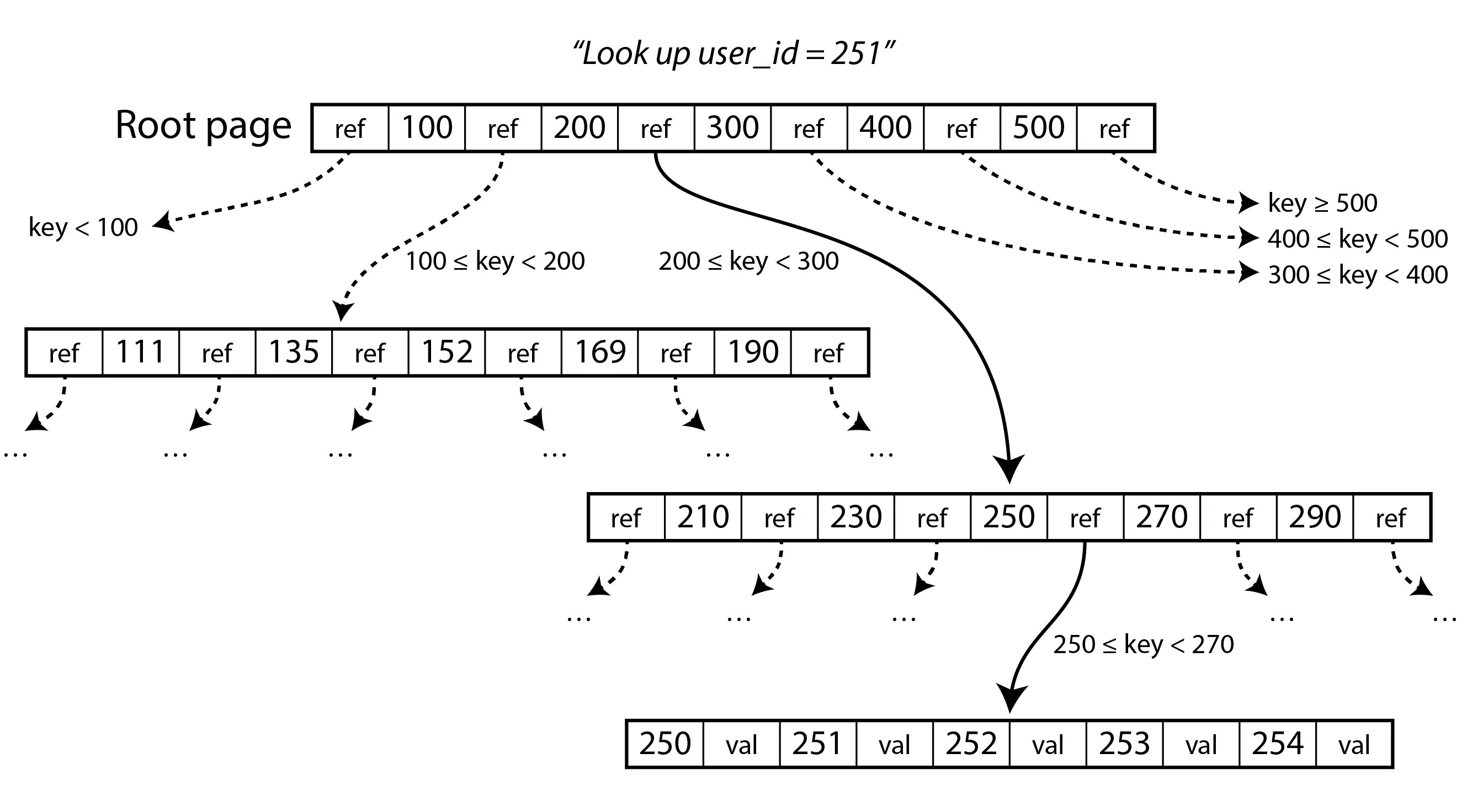B-Tree Veri Yapısı ve Sayfa (Page) Mantığı
İkili ağaçlarda bir düğümün en fazla 2 çocuğu olabiliyordu ancak B-Tree’lerin ana odağı disk performansıdır ve bu nedenle sayfa boyutu el verdiğince çok düğüm (child) olabilir. Ayrıca bir düğümde birden fazla veri noktası bulunmakta. Yukarıdaki resimde 251 numaralı ID’yi arıyoruz. Tek yapmamız gereken, en üst düğümden (root) başlayarak her seferinde uygun aralığı bulmak. Genellikle modern işletim sistemleri en fazla 3-5 okuma çağrısında aranan dosyayı bulmak üzerine dosya sistemini düzenler. Bunun için dallanma faktörü (branching factor) denilen bir değişkeni düzenler. Akılda kalması için şöyle düşünebiliriz; 1500 veriden bir ağaç oluşturmak istediğinizde eğer dallanma faktörü 500 ise yaprak düğüme 3 hamlede ulaşırsınız ama eğer dallanma faktörü 100 ise 15 defa okuma yapmanız gerekir.
Not: Günümüzde B-Tree dediğimizde genellikle B+Tree’lerden bahsedilir. B+Tree’lerde yaprak haricinde veri bulunmaz sadece referans bulunur.
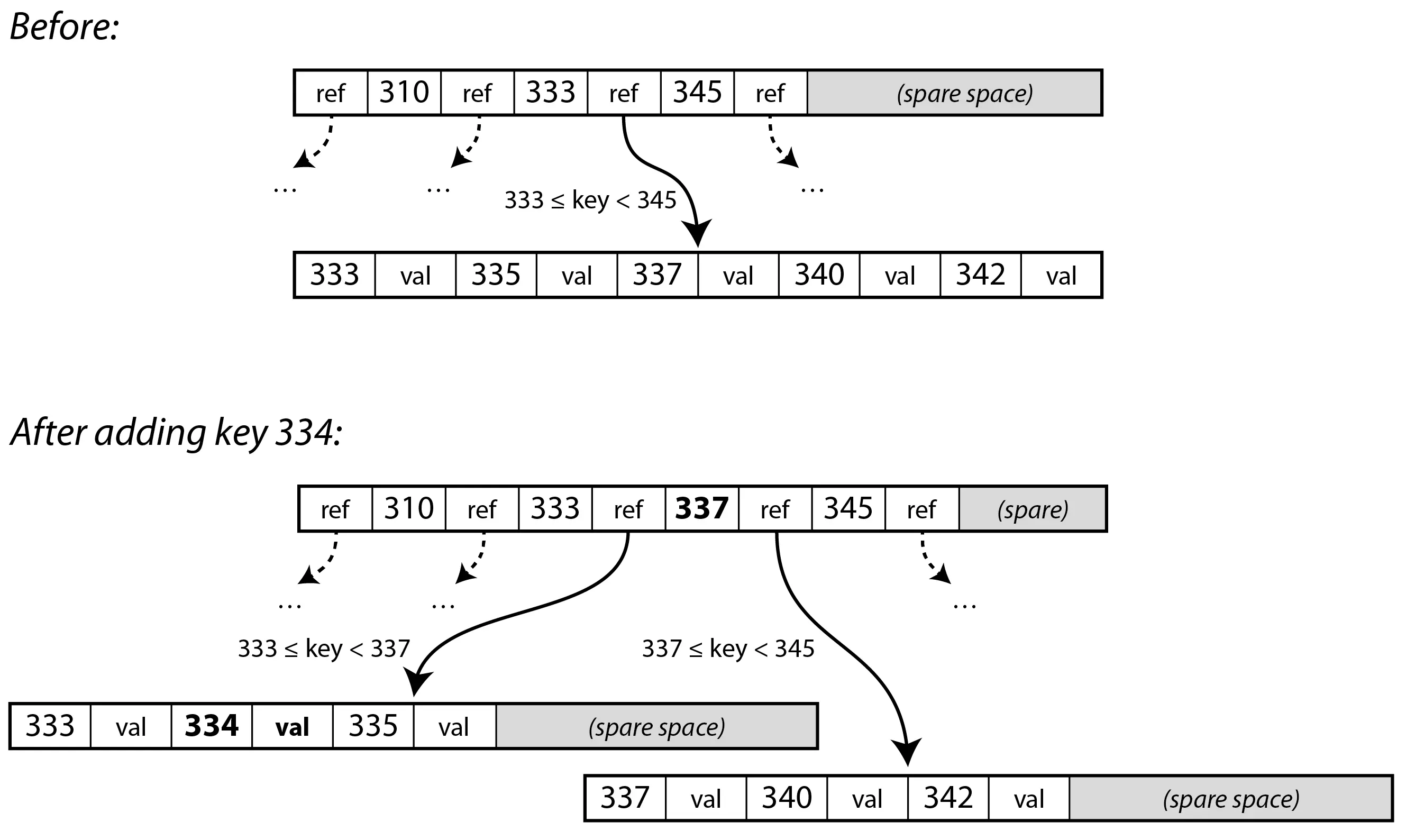B-Tree Bölünme (Page Split) İşlemi
Diyelim ki 334 anahtarını eklemek istiyoruz ancak 333–345 aralığını tutan sayfamızda artık tek bir bitlik bile yer kalmamış. Sistem bu durumda şu adımları izler:
- Böl ve Yönet: Dolu olan sayfa, her biri yaklaşık yarı yarıya dolu olan iki yeni sayfaya bölünür. Örneğimizde, yeni anahtarımızla birlikte
333–337aralığını tutan bir sayfa ve337–344aralığını tutan bir diğeri oluşur. - Yukarıya Rapor Ver: Bu bölünme gerçekleştikten sonra, üstteki ebeveyn (parent) sayfa güncellenir. Artık tek bir referans yerine, bu iki yeni sayfayı ve aralarındaki
337sınır değerini gösterecek iki referansa sahip olur. - Domino Etkisi: Eğer ebeveyn sayfada da yeni referans için yer yoksa, o da bölünür. Bu süreç gerekirse ağacın en tepesine, yani kök (root) düğüme kadar tırmanabilir. Kök düğüm bölündüğünde ise ağacın üzerine yeni bir kök eklenir ve ağaç bir kat daha derinleşir.
Bu durum, B-Tree’yi bildiğimiz ikili arama ağaçlarından ayıran en temel farklardan biridir: B-Tree “aşağıdan yukarıya” doğru büyür. Yani yeni bir veri eklendiğinde ağaç kökten aşağı dallanmak yerine, yapraklardan taşarak yukarıya doğru genişler.
Bu algoritma sayesinde ağaç her zaman dengeli kalır. $n$ adet anahtarı olan bir B-Tree’nin derinliği her zaman $O(\log n)$ mertebesindedir. Pratikte bu şu anlama gelir: 4 KiB’lık sayfalara sahip, 500 dallanma faktörü olan 4 seviyeli bir B-Tree, tam 250 TB veriyi içinde barındırabilir. Yani aradığınız veriye ulaşmak için disk üzerinde sadece 3-4 sayfa atlamanız yeterlidir. Eğer Red-Black ağaçlar ile bunu diskte yapmaya çalışsaydık çok daha fazla hamle yapmamız gerekirdi. Bu nedenle diğer ikili arama ağaçları genellikle bellekte tercih edilir çünkü orada rastgele okuma-yazma hızı inanılmaz yüksektir.
B-Tree’lerde Veri Güvenliği ve Varyantları
B-Tree’lerin en temel operasyonu, diskteki bir sayfayı yeni verilerle tamamen değiştirmektir. Ancak bu, göründüğü kadar basit bir işlem değildir. Bir sayfa bölünmesi (page split) sırasında aynı anda birden fazla sayfayı güncellemeniz gerekir. Eğer tam o anda elektrik kesilirse veya sistem çökerse ne olur?
- Bozulmuş Bir Ağaç: Sayfaların sadece bir kısmı yazılırsa, hiçbir ebeveyni olmayan “yetim” sayfalar oluşabilir ve tüm indeksiniz çöp olabilir.
- Yarım Kalmış Sayfalar (Torn Pages): Donanım tüm sayfayı tek bir seferde (atomik olarak) yazamazsa, sayfanın yarısı eski yarısı yeni kalabilir; buna “torn page” diyoruz.
1. Çözüm: Write-Ahead Log (WAL)
İşte bu riski yönetmek için B-Tree’lerde de LSM-Tree’lerden tanıdığımız bir yöntemi görüyoruz: Write-Ahead Log (WAL). Diskteki sayfaları güncellemeden hemen önce, yapılacak her hamle bu “günlüğe” not edilir. Sistem çökerse, veri tabanı ayağa kalktığında bu günlüğü okur ve ağacı tutarlı eski haline geri döndürür.
2. Çözüm: Copy-on-Write
Bazı veri tabanları (LMDB gibi) ve depolama biçimleri (Linux BTRFS dosya sistemi gibi) ise sayfaların üzerine yazmak yerine, değiştirilen sayfayı tamamen başka bir konuma yazar ve ebeveyn referanslarını oraya yönlendirir. Bu sayede eski veri hiçbir zaman bozulmaz; ya tamamen yeni versiyona geçilir ya da eski versiyon sağlam kalır.
Temel B-Tree yapısı, yıllar içinde disk performansını daha da artırmak için çeşitli optimizasyonlara uğramıştır. Burada iki tanesine değineceğim:
- Abbreviated Keys (Kısaltılmış Anahtarlar) adı verilen bir yöntem ile özellikle ağacın iç sayfalarında tüm anahtarı saklamak yerine, sadece sınırları belirleyecek kadarını saklarız. Bu sayede bir sayfaya daha fazla anahtar sığar, dallanma faktörü artar ve ağaç daha da sığlaşır; bu da bizi aradığımız veriye daha hızlı götürür.
- Bazı B-ağacı uygulamaları, yaprak sayfalarını diskte sıralı (sequential) olması için ağacı düzenlemeye çalışır ve böylece disk arama sayısını azaltır. Ancak, ağaç büyüdükçe bu sırayı korumak zordur.
LSM-Trees vs B-Trees
Genel geçer kural şudur: LSM-Tree’ler yazma yoğunluklu (write-heavy) işler için, B-Tree’ler ise okuma yoğunluklu (read-heavy) işler için daha uygundur. Ancak Kleppmann bizi uyarır: Benchmark testleri, sizin iş yükünüzün detaylarına göre çok hassastır; yani kendi senaryonuzu test etmeden karar vermeyin.
1. Performans Kriterleri
- Okuma Hızı: B-Tree’ler bu konuda daha öngörülebilirdir. Ağacın derinliği bellidir, kaç sayfa okuyacağınız bellidir. LSM tarafında ise aradığınız veri MemTable’da yoksa, diskteki farklı segmentlere bakmanız gerekir (Bloom Filter burada hayat kurtarır ama B-Tree istikrarını 50 yılı aşkın geçmişinden alır).
- Sıralı ve Rastgele Yazma: B-Tree’ler veriyi güncellemek için diskteki rastgele sayfalara gider (Random Write). LSM-Tree ise veriyi her zaman dosyanın sonuna ekler (Sequential Write). Özellikle mekanik disklerde (HDD) sıralı yazma, rastgele yazmaya göre katbekat hızlıdır. SSD’lerde bu fark azalsa da, LSM’in sıralı yazma mantığı hala ciddi bir avantaj sağlar.
2. Write Amplification (Yazma Çoğaltması)
Her veri tabanı, siz “bir birim” veri yazdığınızda diske “birden fazla birim” veri yazar (Log dosyası, indeks güncellemesi vb.). Buna Write Amplification (Yazma Çoğaltması) denir. LSM-Tree’ler genellikle yazma sırasında daha az hamle yapar çünkü veriyi sıkıştırarak sıralı yazarlar. B-Tree’ler ise bazen sadece birkaç byte’lık bir değişim için 4 KiB’lık koca bir sayfayı yeniden yazmak zorunda kalır. Eğer SSD ömrü veya yazma bant genişliği sizin için kritikse, LSM bir adım öne çıkar.
3. Disk Alanı ve Parçalanma
B-Tree sayfaları her zaman %100 dolu değildir; bölünmelerden dolayı sayfalarda boşluklar kalır (Fragmentation / Parçalanma). LSM-Tree’ler ise düzenli olarak yapılan Compaction işlemi sayesinde eski ve silinmiş verileri temizler, diskte daha az yer kaplar ve sıkıştırma (compression) algoritmalarıyla çok daha verimli çalışır.
Secondary Indexes (İkincil İndeksler)
Şu ana kadar hep “Primary Key” (Birincil Anahtar) üzerinden konuştuk. Yani id=42 olan veriyi getirdik. Peki ya “İsmi Tunahan olan kullanıcıları getir” dersek? İşte burada Secondary Indexes (İkincil İndeksler) devreye girer.
İkincil indekslerin en büyük farkı, anahtarların benzersiz (unique) olmak zorunda olmamasıdır. Birçok kullanıcının ismi “Tunahan” olabilir. Veri tabanları bunu çözmek için iki yol izler:
- Heap File (Yığın Dosyası): İndeks, verinin kendisini tutmaz. Sadece verinin diskte nerede durduğuna dair bir adres (pointer) tutar. Verinin aslı, sırasız bir yığın (heap) içinde durur. Bu yöntem, veriyi güncellemek istediğinizde (eğer boyutu değişmiyorsa) indeksleri güncellemek zorunda kalmadığınız için verimlidir.
- Clustered Index (Kümelenmiş İndeks): Verinin tamamını doğrudan indeksin içinde saklar. Okuma yapmak inanılmaz hızlıdır (ekstra bir yere gitmenize gerek kalmaz), ama veriyi kopyaladığınız için diskte çok yer kaplar ve yazma maliyetini artırır. MySQL’in InnoDB motorunda Primary Key her zaman bir Clustered Index’tir.
- Covering Index: Bu ikisinin ortasıdır. Verinin tamamını değil, sadece çok sık sorulan bazı sütunları indeksin yanına iliştirir.
Her Şeyi RAM’de Tutmak: In-Memory Databases
Yıllarca disklerin yavaşlığıyla, karmaşıklığıyla uğraştık. Ancak artık RAM fiyatları eskisi kadar yüksek değil ve veri setlerimiz (bazen) tamamen RAM’e sığabilecek boyutlarda kalıyor. Bu da In-Memory (Redis, Memcached, VoltDB) veri tabanlarının yükselişini getirdi.
Burada çok yaygın bir yanlış anlaşılma vardır: “In-Memory veri tabanları hızlıdır çünkü diskten okuma yapmazlar.” Hayır, asıl sebep bu değil. İşletim sistemi zaten sık kullanılan disk bloklarını RAM’de (cache) tutar. In-Memory veri tabanlarının asıl hız farkı, veriyi diske yazılacak formata (encoding/serialization) sokmak zorunda kalmamalarından gelir. Veri, bellekte nasıl duruyorsa öyle işlenir; pointer’lar ve nesneler doğrudan kullanılır.
1
2
3
4
5
6
❯ free -h
total used free shared buff/cache available
Mem: 15Gi 7.1Gi 1.2Gi 210Mi 7.7Gi 8.4Gi
Swap: 23Gi 1.3Gi 22Gi
# Kapattığınız uygulamalar (ve nesneler) tamponda (buffer) bekletilir.
# Unutmayın "unused RAM is wasted RAM".
Peki elektrik giderse? RAM uçucudur. Bu yüzden “In-Memory” olsalar bile, dayanıklılık (durability) iddia eden sistemler veriyi diske bir append-only log olarak yazmaya devam ederler veya düzenli aralıklarla diske “snapshot” alırlar. Disk burada aktif okuma için değil, sadece bir felaket anında veriyi kurtarmak için “kara kutu” olarak kullanılır.
Son Söz: Gümüş Kurşun Yoktur
Yazının başına, Fred Brooks’un sözüne dönelim. B-Tree veya LSM-Tree, Heap File veya Clustered Index… Hiçbiri diğerinden mutlak üstün değildir. Eğer öyle olsaydı en başından diğerlerinin üstünü çizmiş olurduk ama bugün hepsinin pazar payı birbirine inanılmaz yakın.
Veri yoğunluklu bir dünyada mühendislik, “en iyiyi” seçmek değil, projenizin hangi acıya katlanabileceğine karar verme sanatıdır.