Aradığınız 'FuneralCS yazısı' ile ilgili hiçbir arama sonucu mevcut değil

Aradığınız Yazı Bulunamadı: Google’ın Göremediği Yerler

Uyarı: Bu yazı aslında o aradığınız yazı ama arattığınızda, karşınıza yine “Aradığınız ‘FuneralCS yazısı’ ile ilgili hiçbir arama sonucu mevcut değil.” çıkacak. Ve o sonuç, işte şu an okuduğunuz yazının ta kendisi; yani bulamadığınız bir şeyi okuyacaksınız…

Editör Notu: Bu yazı ilerledikçe giderek daha teknik bir yapıya bürünmektedir. İlk bölümler herkesin rahatlıkla takip edebileceği şekilde sadeleştirilmiş; ilerleyen kısımlarda ise makine öğrenmesi, embedding ve retrieval gibi daha teknik konulara girilmiştir. Eğer yalnızca genel fikir edinmek istiyorsanız giriş ve ilk bölümler yeterli olacaktır.

Hiç Google’da aradığınız şeyi bulamadığınız oldu mu? Sıralamada gerilerde olmasından bahsetmiyorum. Hani şu ekran var ya, işte bugünün konusu tam olarak bu ekranın teknik ve matematiksel sebebi:

Google'ın o meşhur "çaresiz" balıkçısı.

PageRank: Her Şeyin Başlangıcı

Larry Page ve Sergey Brin, doktora yaptıkları sırada “dünyadaki bilgiyi organize etmek ve evrensel olarak erişilebilir hale getirmek” gibi devasa bir hedefle Google’ı kurdu. İlk kurguladıkları algoritma aslında oldukça basitti; Googlebot (web crawler) önce bilinen büyük sitelerden başlar, sayfaları indirir, içindeki linkleri çıkarır ve bu döngüyü sonsuza kadar tekrarlar.

Meraklısına: Peki bu kadar büyük bir ağı taramak çok uzun sürmez mi? Bir haber sayfası yeni içerik girdiğinde neden neredeyse anında arama sonuçlarında görebiliyoruz? Buraya birazdan, modern yöntemlere geçtiğimizde döneceğiz.

Sıralama kısmında ise efsanevi PageRank devreye giriyordu. Akademik dünyada bir makalenin değeri nasıl aldığı atıflarla ölçülüyorsa; Google da aynı mantığı web sitelerine uyguladı. Bir sayfa başka sitelerden ne kadar çok link alıyorsa, arama sonuçlarında o kadar değerli sayılıyordu. Üstelik popüler sitelerden gelen linkler, sıradan sitelerden gelenlerden daha “ağır” basıyordu.

Ancak bu sistemin ciddi dezavantajları vardı:

• Hiç link almayan siteler içerikleri ne kadar iyi olursa olsun neredeyse görünmez kalıyordu.

• Manipülasyona çok açıktı; link satın alarak sıralama şişirilebiliyordu veya çok basit teknikler vardı (Wikipedia’da herhangi bir yazıda kendi sitenize atıf yapmak gibi).

• Tazelik (Freshness) ve Konu Sapması (Topic Bias) sorunları nedeniyle güncel veya çok niş içerikler geri planda kalabiliyordu.

Google bu yüzden zamanla PageRank’in yanına yüzlerce farklı sinyal eklemek zorunda kaldı.

---

PageRank algoritmasında atıfların site ölçeğine göre etkisi.

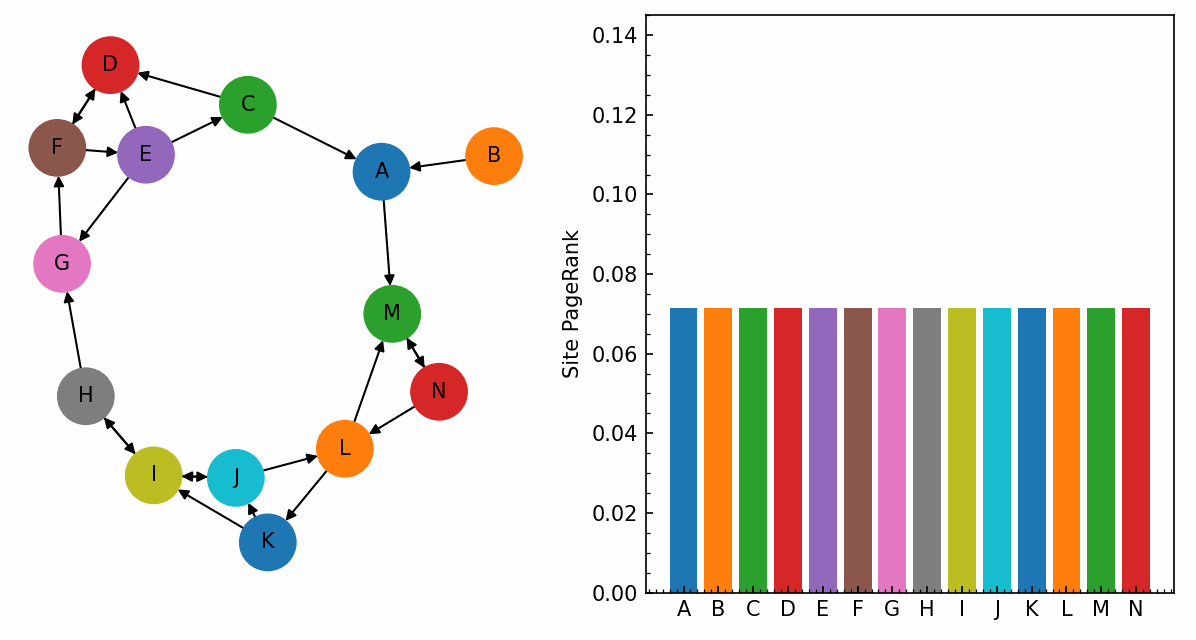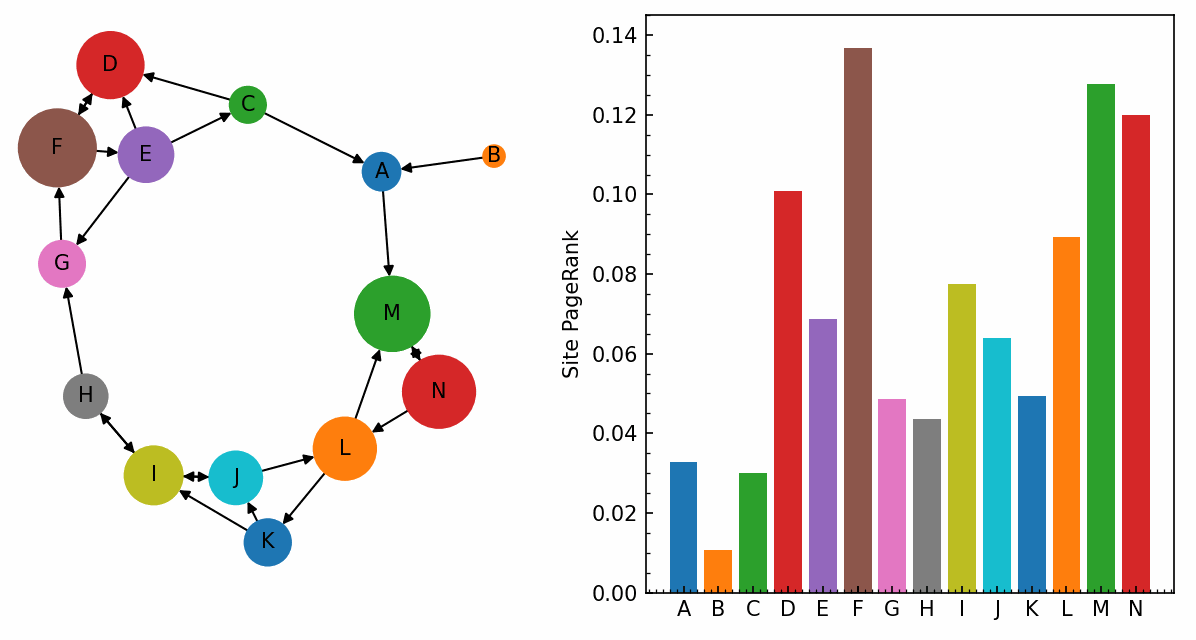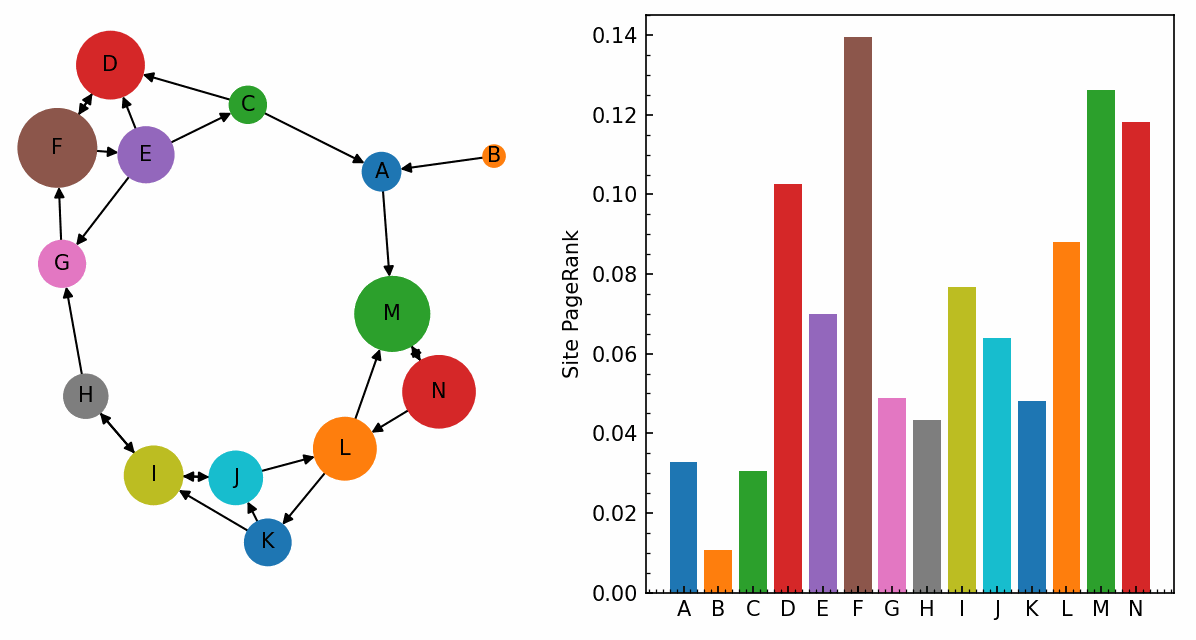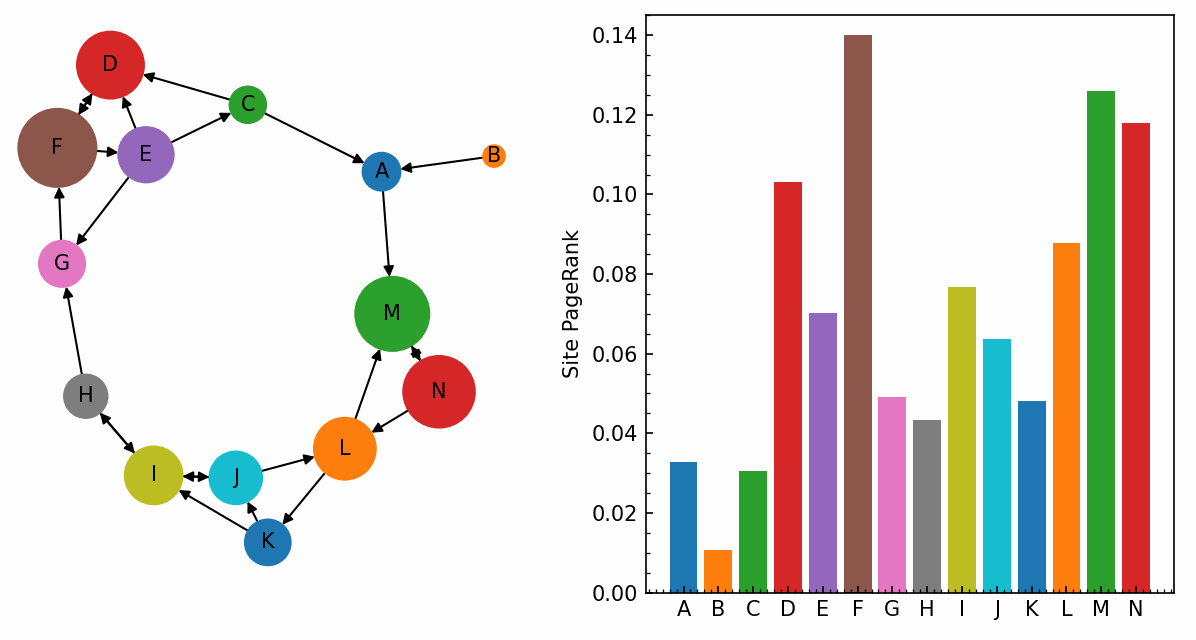
Şu anki sistem ise çok daha akıllı ve AI araçlarını da yoğun bir şekilde kullanıyor. Haber siteleri gibi anlık güncellenmesi gereken siteleri crawler araçlar belki de her saniye tekrar tekrar tarıyor ve dizini güncelliyor.

Artık sadece link değil; içerik kalitesi, güncellik, güvenilirlik, spam kontrolü, kullanıcı niyeti ve daha pek çok parametreyi kullanıyor Google.

RankBrain, BERT, MUM, neural matching ve daha pek çoğu… Bu terimlerin hepsi, kaynakçada da yer verdiğim “Google Arama sıralama sistemleri kılavuzu” içerisinde mevcut. Ama biz bu yazıda orada yer alan “BERT” ve türevlerinin her şeyi nasıl “temsil edemediğine” değineceğiz.

LIMIT: Google’ın Kendi Mühendislerinden İtiraf

Konuyla ilgili incelediğimiz makale, bizzat Google DeepMind ekibinden (baş yazar Orion Weller) çıkıyor. Yani Google’ın arama motoru paradigmasının sınırlarını çizen makale, yine içeriden geliyor. Çalışmanın adı manidar: LIMIT.

Yazarlar, çok basit bir soru soruyor: “Bir yapay zeka modeli, kelimeleri sayılara (vektörlere) dönüştürürken neleri kaybeder?”. Yazı, vektörlerin temsil yeteneğini anlatarak başlıyor. Ardından eski çalışmalar ile bazı şeylerin neden temsil edilemediğini gösteriyor.

Bu makalenin en çarpıcı yanı ise şu: İlkokuldaki okumayı öğreten fişlerdeki basit cümlelerle bile, devasa embedding sistemlerinin nasıl çıkmaza girebildiğini kanıtlıyor. Üstelik çalışma çok küçük sıralama değerleriyle yapılmış, yani modelden yalnızca 2 tane cümleyi doğru sıralaması isteniyor.

LIMIT Dataseti: Kim neyi seviyor?

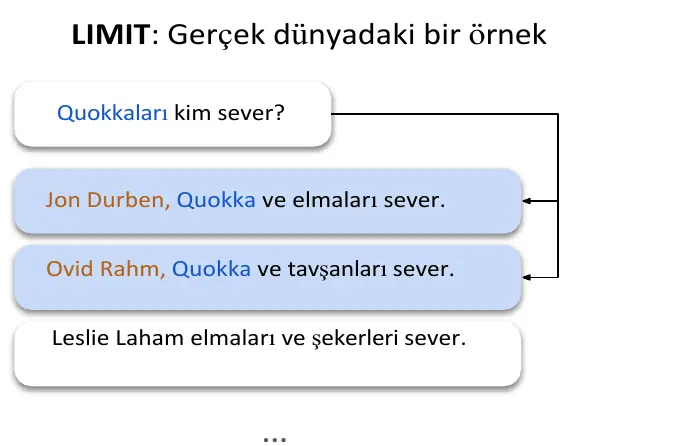
Ufak bir bilgi: Quokka, Avustralya’da yaşayan kısa kuyruklu bir kanguru türüymüş. Fotoğraflarda hep gülüyormuş gibi çıkarlar, oradan hatırlarsınız. 😅

Öncelikle embedding kavramına çok kısa değinelim.

Bilgisayar her şeyi sayılarla anlar. Dolayısıyla bir şeyi bilgisayara öğretmek için, onu sayılarla temsil etmek gerekir.

Mesela çok basit bir yöntem düşünelim: elma = 1, armut = 2, araba = 3.

Bu şekilde etiketlersek, bilgisayar “armut > elma” (2 > 1) gibi anlamsız bir matematiksel büyüklük karşılaştırması yapabilir. Ya da 1–2–3 ardışıklığı yüzünden, “araba da meyvelerin bir benzeri galiba” sonucunu çıkarabilir çünkü sayısal uzayda yan yanalar. Yani bu temsil hiçbir gerçek anlam taşımıyor (bkz. “Label Encoding”).

İşte Embedding bu yüzden tek boyutlu etiketlerden ibaret olamaz. Bunun yerine çok boyutlu uzaylar kullanıyoruz. Her kelime veya nesne, çok boyutlu bir vektör (veya tensör) ile temsil ediliyor. Her boyut, nesnenin farklı bir özelliğini (feature) yansıtıyor. Böylece “elma” ile “armut” uzayda birbirine yakın konumlanırken, “araba” bambaşka bir koordinatta durabiliyor.

Embedding uzayı hakkında görselleştirme

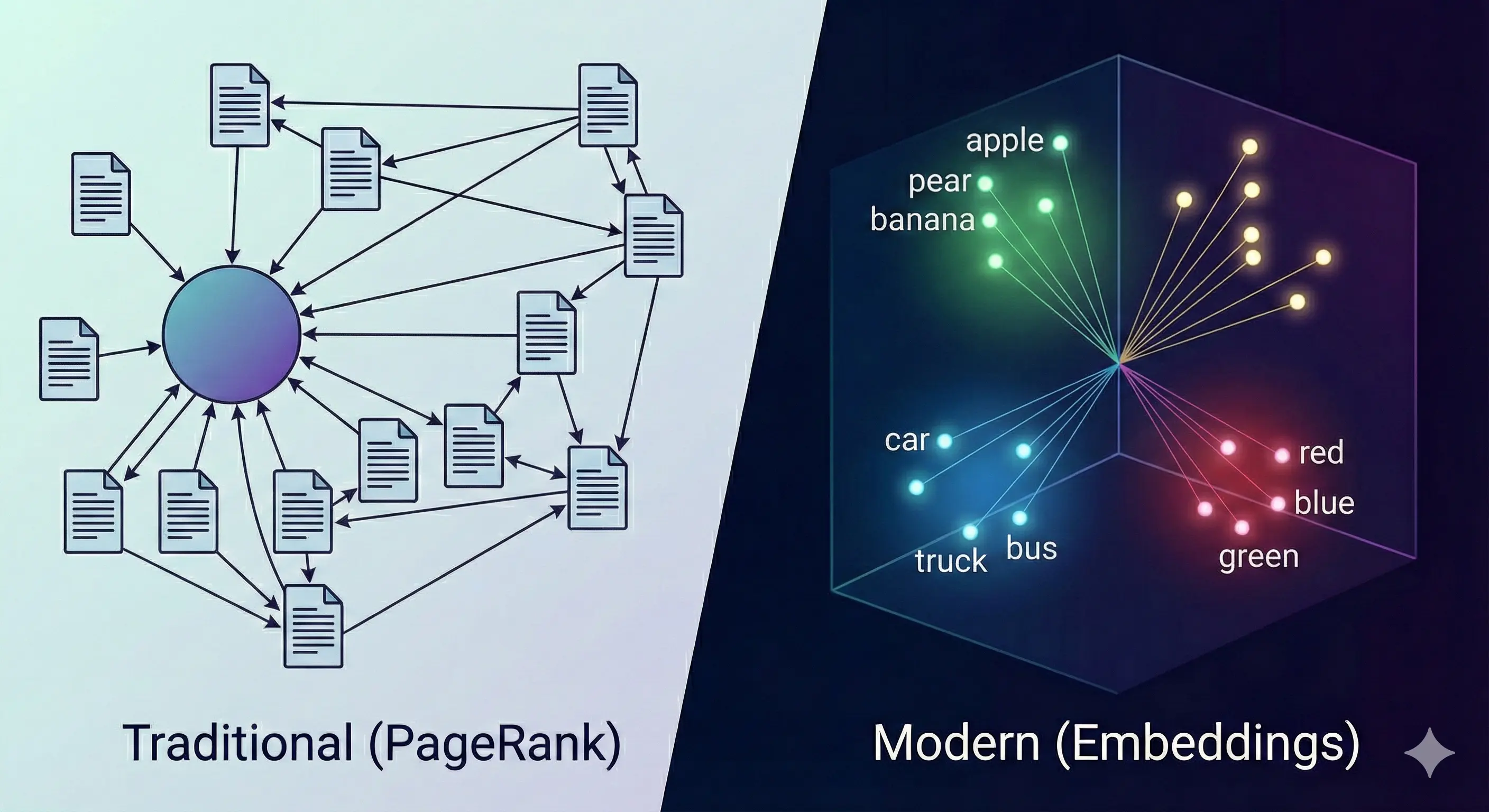
Peki öyle şeyler var mıdır ki hiçbir şekilde matematik ile temsil edilemez veya ayrıştırılamaz? Mesela yukarıdaki Quokka görselindeki mantığı bilgisayar ne kadar iyi ayırt edebilecek? Gelin, bir metni “gömmeyi” (embedding) deneyelim.

Örneğin bu yazımızın başlığını sizler için “SBERT” ile gömmeyi deneyeceğim. Basit bir kod ile başlayalım:

Kod geliyor! 😅 Merak etmeyin, anlamak için uzman olmanız gerekmiyor; biraz yazılım okuryazarlığı işinizi görecektir. Gerekli yerlere açıklama bıraktım.

from sentence_transformers import SentenceTransformer

model = SentenceTransformer('sentence-transformers/all-mpnet-base-v2') 
# Bunu Google sorgusunu bilgisayara anlatan tercüman/dönüştürücü gibi düşünebiliriz.

text = "Aradığınız 'FuneralCS yazısı' ile ilgili hiçbir arama sonucu mevcut değil" 
# Bu ise Google'a olan sorumuz.

embedding = model.encode(text)
print("Vektörün boyutu:", len(embedding))

print("İlk 10 değer:", embedding[:10])

# ÇIKTI:
# Vektörün boyutu: 768 
# (Tüm cümlenin bilgisayar için ifade ettiği anlam uzunluğu - bunu biz belirledik aslında)
# İlk 10 değer: [ 0.08241844 -0.00802192 -0.00111354  0.03817566 -0.0503126   0.00824948
#   0.04679048  0.01312113  0.01456734  0.01648803] 

Peki cümleyi birazcık değiştirip şöyle yapalım:

text = "Aradığınız  'Yazı' ile ilgili hiçbir arama sonucu mevcut değil"
embedding2 = model.encode(text)

# Vektörün boyutu: 768
# İlk 10 değer: [ 0.03601046 -0.01979215 -0.01988745 -0.00076254 -0.03193635  0.03404633
#   0.0785526   0.01048531  0.02877098  0.01428796]

# Şimdi de Cosine Similarity hesaplayalım (vektörler arasındaki açının kosinüs değeri):
import torch
from torch.nn.functional import cosine_similarity

embedding = torch.tensor(embedding, dtype=torch.float32).unsqueeze(0) 
# Kosinüs hesaplamak için vektörü tensörlere çevirmeliyiz, bu kısımlar saf matematik.

embedding2 = torch.tensor(embedding2, dtype=torch.float32).unsqueeze(0)

print(cosine_similarity(embedding, embedding2))

# ÇIKTI:
# tensor([0.7448])

Yani bilgisayar bu iki cümleyi %74.48 benzer buldu.

Peki şöyle yaparsak ne olur?

text = "Aradığınız 'FuneralCS' ile ilgili hiçbir arama sonucu mevcut değil"
embedding3 = model.encode(text)

# Vektörün boyutu: 768
# İlk 10 değer: [ 0.0866233  -0.01295199 -0.0074097   0.03779288 -0.05800581  0.00488742
#   0.05130353  0.01200954  0.02305291  0.01696091]

print(cosine_similarity(embedding, embedding3))

# ÇIKTI:
# tensor([0.9841])

Gördüğümüz üzere %98.41 benzer çıktı.

Ama biz sorgulardan birinde siteyi (FuneralCS), birinde ise sitenin içindeki yazıyı aradık. Aradaki fark bizim için büyük ama bilgisayar için neredeyse yok hükmünde.

LIMIT dataseti de tam olarak bu soruna odaklanıyor. Belirli bir $n$ boyutu için (örneğin 768 boyutlu bir vektör), %100 doğruluk ile temsil edilebilecek (yani hatasız sıralanabilecek) doküman sayısı kaçtır?

Tamam, belki bizim 3 cümlemiz arasından bir sorgu vektörü ile sıralama yapmak kolay ancak Google milyarlarca varyasyonun olduğu bir veri kümesinden “retrieval” (geri getirme) yapıyor.

Retrieval: Bilgisayar biliminde “geri getirme / bulup çıkarma” demektir. Yani bir veritabanından, kullanıcının sorgusuna en uygun vektörün bulunup sunulması işlemidir.

Yukarıda da gördüğümüz üzere benzer görünen cümleler bazen %74 çıkıyor, bazen %98; ama bu farkın ne zaman kritik olduğu asıl büyük soru.

Makalede denenen modellerin hepsi son teknoloji (SoTA - State of Art) modeller. Çalışma learning theory ve communication complexity temellerine dayanıyor.

Learning theory (öğrenme süreçlerini matematiksel olarak inceleyen alan) ve communication complexity ise bir problemi çözmek için sistemler arası gereken bilgi alışverişinin ölçümüdür.

Modelin boyutunun sınırlayıcı bir faktör olduğunu ve boyut arttıkça performansın da arttığını görüyoruz. Ancak çok vektörlü modellerin bile zorlandığını görüyoruz.

Burayı biraz detaylı açıklamam iyi olacaktır: Recall (Geri Çağırma)

Bilgi getirme (information retrieval) sistemlerinde performansı ölçmek için kullanılan en temel metriklerden biridir.

• Recall = Sistemin “ilgili” dokümanların kaçını bulabildiği.

• @k = İlk k sonuç içinde.

Diyelim ki sorgun var: “FuneralCS yazısı”

• Gerçekte bu sorguyla alakalı veritabanında 3 doküman var.

• Sistem sana bir sıralama döndürdü: [Dok1, Dok2, Dok3, Dok4, Dok5 …]

Şimdi senaryoya bakalım:

• Eğer ilk 2 sonuç [Dok1, Dok4] ise → Alakalı 3 dokümandan sadece 1 tanesi ilk 2’ye girmiş.

  • Recall@2 = 1/3 ≈ 0.33 -> %33 Başarı.

• Eğer ilk 2 sonuç [Dok1, Dok2] ise → Alakalı dokümanlardan 2 tanesi ilk 2’de.

  • Recall@2 = 2/3 ≈ 0.66 -> %66 Başarı.

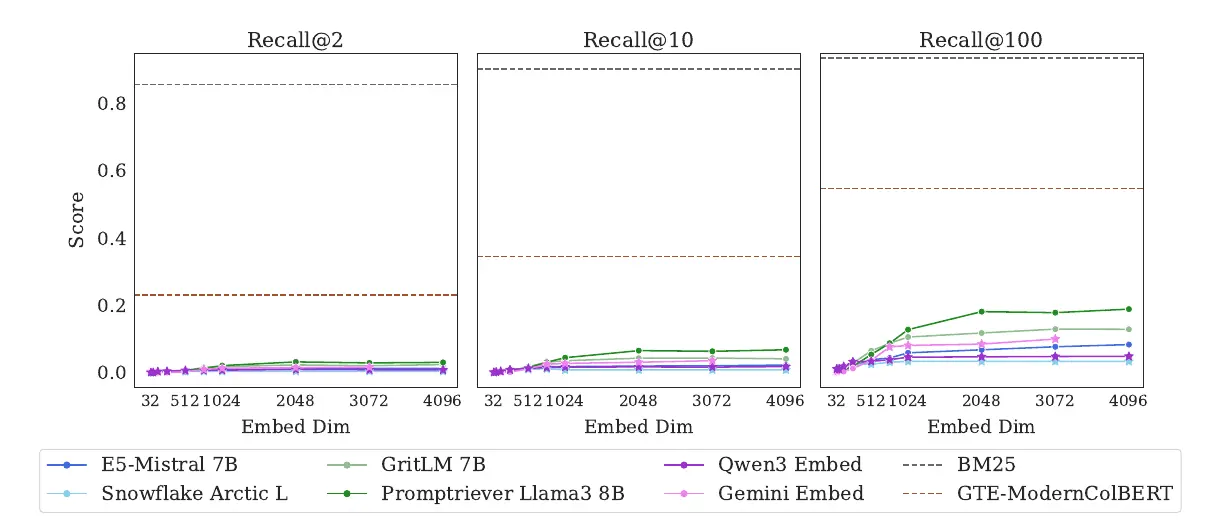
Gördüğümüz üzere sonuçlar çok şaşırtıcı. Görev son derece basit olmasına rağmen (Quokka’nın sevdiği yiyecekler) devasa modeller zorluklar yaşıyor. Bu açıkça şu anlama geliyor: Gömmeler (embeddings) çok sayıda kombinasyonu temsil edebilir, ancak tüm kombinasyonları temsil edemez veya en azından belirli bir $k$ değerinde çağırılabileceğini garanti edemez.

Alternatif Teknikler ve Mimariler

Peki bu işin çözümü yok mu? Araştırmacılar alternatiflere de bakmışlar:

Encoder'ların farkları

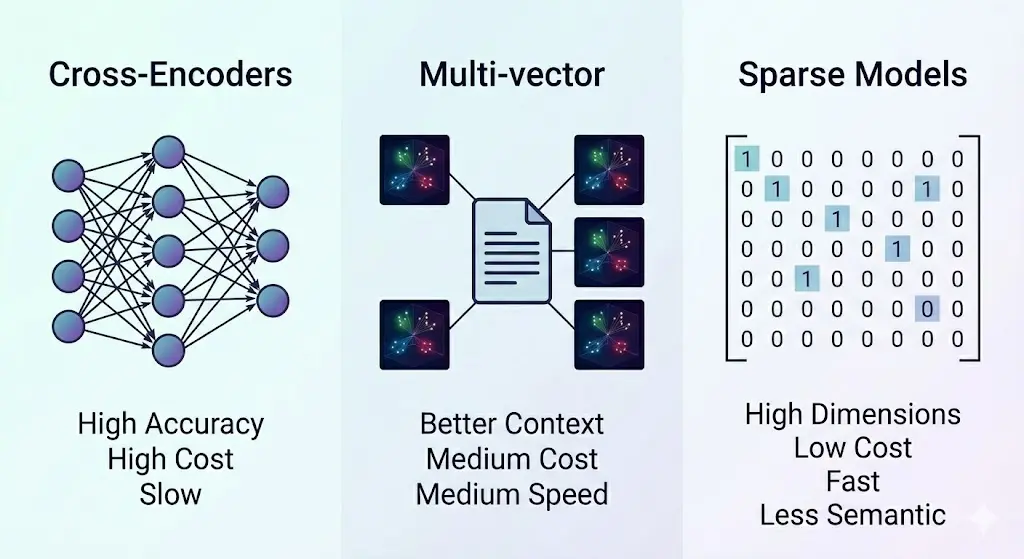
1. Cross-Encoders (Çapraz Kodlayıcılar)

• Normalde “ilk aşama retrieval” (milyonlarca dokümandan birkaç yüz aday seçme) için uygun değillerdir. Çünkü çok pahalıdır (hesaplama maliyeti çok yüksek).

• Genellikle “reranking” (ilk aşamadan gelen 100 adayı tekrar, daha hassas sıralamak) için kullanılırlar.

• LIMIT dataseti üzerinde Gemini-2.5-Pro denenmiş:

  • Ona tüm 46 doküman + 1000 query tek seferde verilmiş.

  • %100 başarıyla doğru eşleşmeleri bulmuş (ilgili makalenin Cross-Encoders kısmında bulabilirsiniz).

• Yani LIMIT dataseti, embedding modelleri için bir kabus olsa da, cross-encoder için “çocuk oyuncağı”. Ama maliyet ve hız yüzünden tüm Google aramalarında en başta kullanılamaz.

2. Multi-vector Modeller

• Normal embedding modellerinde → Doküman tek bir vektörle temsil edilir.

• Multi-vector modellerde → Her doküman birden fazla vektör ile temsil edilir (örneğin ColBERT).

Örnek:

• Doküman: “kırmızı renkli bir araba gördüm”

• Sorgu: “kırmızı renk”

  • “kırmızı” (sorgu) ↔ “kırmızı” (doküman) = 1/5

  • “renk” (sorgu) ↔ “renkli” (doküman) ≈ 0.8/5

  • Toplam skor ≈ 1.8/5

Bu yöntem sayesinde, SBERT gibi tek vektörlü modellerde kaybolan “kırmızı renkli” ayrımı korunmuş olur.

3. Sparse (Seyrek) Modeller

• BM25 gibi “klasik” yöntemler aslında dense modellerin aksine çok yüksek boyutlu vektörler kullanır (her kelime = bir boyut).

• Her kelime bir boyuttur → Vektörün boyutu = Bütün kelime haznesi (milyonlarca olabilir).

• Sorgu ve doküman = Kelime frekanslarına göre sparse (çoğu değer 0’dır).

• Skor = Kelime örtüşmesine göre hesaplanır (TF-IDF türevi).

• Bir de bunun nöral ağlardaki hali vardır (SPLADE vb.).

• Çok büyük olduğu için teorik embedding limitlerine takılmıyor gibi görünür ama anlam eşlemesi zayıftır (Eş seslileri karıştıran TF-IDF yapısına benzer).

Boyut başına doğruluk sınırları: Kritik N Noktası.

Peki Google Bu Yazıyı Bulabilecek mi?

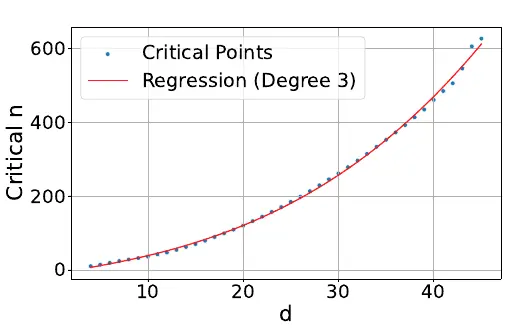
Bulamayabilir. Çünkü araştırmacılar her embedding boyutu (d) için bir “kritik n noktası” tanımlıyor.

Bu nokta, modelin tüm kombinasyonları doğru temsil edemeyeceği doküman sayısını gösteriyor.

Başka bir deyişle: Boyut ne kadar küçükse, modelin “ayırt edebileceği” doküman sayısı da o kadar sınırlı.

Örneğin:

• d = 512 → yaklaşık 500 bin doküman

• d = 768 → 1.7 milyon doküman

• d = 1024 → 4 milyon doküman

• d = 3072 → 107 milyon doküman

• d = 4096 → 250 milyon doküman

Bu ilişkiyi şöyle bir polinom fonksiyonla modellemişler ($y$ burada açıklanabilir doküman sayısıdır):

\(y = -10.5322 + 4.0309d + 0.0520d^2 + 0.0037d^3\)

Yani boyut (d) büyüdükçe ayırt edilebilecek doküman sayısı hızla artıyor. Ama unutmayalım: Bu hesap ideal koşullar için geçerli. Yani modelin doğrudan test setine optimize edilip dil kısıtları olmadan çalıştığı “free embedding” durumu. Gerçek dünyadaki dil modelleri, doğal dilin karmaşıklığı nedeniyle bu sınırların çok altında performans gösteriyor. {: .prompt-info }

Kişisel fikrim şu ki; bugün Google bazı yazıları bulamıyor olabilir. Ama multi-vector modeller ve hibrit sistemler, gelecekte bu yazının bile Google’da kolayca bulunabilmesini mümkün kılacak.

Ancak şu haliyle Google’ın dizinindeki doküman sayısını (gezegen boyutunda) düşünürsek işimiz biraz zor gibi. Yani belki de bu yazı, gerçekten Google’ın bulamayacağı bir yazıdır. Ama siz buldunuz. Belki bir başkasının bulmasına da yardımcı olursunuz.

Merak edenler için tüm kodu çalıştırabileceğiniz bir Colab dosyası hazırladım: Colab Notebook

Kaynakça ve İleri Okuma

1. PageRank Örneği – Wikipedia
2. Google Arama Sıralama Sistemleri Kılavuzu
3. On the Theoretical Limitations of Embedding-Based Retrieval