Entropiyi Anlamak - Karmaşanın Matematiği
Entropinin termodinamikten Shannon entropisine ve yapay zekaya uzanan rolü: karar ağaçları, cross-entropy loss ve PCA örnekleriyle karmaşanın matematiği.
Entropiyi Anlamak: Karmaşanın Matematiği
Neden sürekli oturmak ve iş yapmamak isteriz? Çünkü otururken görece daha az enerji harcarız ama bu sefer de hiçbir iş yapmadığımız için hayatımız daha düzensiz bir hal almaya başlar. Entropi, bir sistemin düzensizliğinin ve rastgeleliğinin ölçüsü olarak tanımlanabilir. Evrende her şey, kendini minimum serbest enerjiye çekmek ister. Bu da yanında düzensizliği getirir (ve tam tersi de). Bu bilim dünyasında kuantum mekaniği ile birlikte en çok araştırılan husus olmuştur.
Önce bu işin kalbine yani termodinamiğe bir bakış atalım.
Termodinamik
Termodinamik, ısı, iş, sıcaklık ve enerji arasındaki ilişkiyi inceleyen bilim dalıdır. Bu bilim dalı, genel olarak bir yerden başka bir yere ve bir formdan başka bir forma enerji transferini inceler. Temel kavram, ısının belirli bir miktar mekanik işe karşılık gelen bir enerji formu olduğudur.
Isı, 1798 yılına kadar resmi olarak bir enerji türü olarak kabul edilmiyordu. Bu tarihte, İngiliz askeri mühendis Kont Rumford, top namlularının delinmesinde sınırsız miktarda ısı üretilebileceğini ve üretilen ısı miktarının, keskin olmayan bir delme aletini döndürmek için yapılan iş ile orantılı olduğunu fark etti. Rumford’un üretilen ısı ile yapılan iş arasındaki orantılılık gözlemi, termodinamiğin temelini ve birinci yasasını oluşturur.
İkinci yasa ise Alman bilim insanı Rudolf Clausius, tarafından “Isı, hiçbir zaman soğuk bir cisimden ılık bir cisme bir takım değişiklikler olmadan geçmez.” diyerek konulmuştur.
Bu yasa, izole bir sistemin toplam entropisinin zamanla asla azalmayacağını, aksine sürekli olarak artma eğiliminde olduğunu belirtir. Bu, evrenin doğal olarak daha düzensiz veya rastgele bir duruma doğru ilerlediği anlamına gelir. Bu bağlamda entropi, bir sistemdeki faydalı (iş yapabilir) enerji miktarı azaldıkça artar. Termodinamiğin ikinci yasası, entropinin tanımlanmasını sağlamıştır. Fiziksel olayların neden tek yönlü olduğu (örneğin, kırılan bir bardağın kendiliğinden birleşmemesi), entropinin sürekli artmasıyla açıklanır.
Termodinamik yasaları çok genel bir geçerliliğe sahiptirler ve karşılıklı etkileşimlerin ayrıntılarına veya incelenen sistemin özelliklerine bağlı olarak değişmezler. Yani bir sistemin sadece madde veya enerji giriş-çıkışı bilinse dahi bu sisteme uygulanabilirler.

bilgi teorisi ve Shannon Entropisi
bilgi teorisi, bilginin niceliklendirilmesi, depolanması ve iletilmesinin uygulamalı matematik ve elektrik mühendisliği dalıdır. Bu alan, 1940’larda Claude Shannon tarafından kurulmuş ve geliştirilmiştir. bilgi teorisinin temel konularının uygulamaları arasında kaynak kodlama/veri sıkıştırma (örneğin ZIP dosyaları) ve kanal kodlama/hata algılama (channel coding/error dedection) ve düzeltme (örneğin DSL) yer almaktadır.
Entropi 20. yy’da Shannon tarafından bilgi teorisine kazandırılmıştır. Shannon, entropiyi, bir iletinin veya olayın içerdiği bilgi miktarını veya daha doğrusu tahmin edilemezliğini ve belirsizliğini ölçmek için kullanmıştır.
bilgi teorisinde entropi, fizikten biraz farklı olarak bir sonucun ne kadar belirsiz veya sürprizli olduğunun bir ölçüsüdür. Bir yazı tura atışında, paranın yazı mı tura mı geleceği belirsizdir, dolayısıyla bu olayın entropisi maksimumdur. Eğer paranın hileli olduğunu ve %75 olasılıkla tura geldiğini biliyorsak, sonuç hakkındaki belirsizliğimiz azalır ve entropi de düşer.
Benzer şekilde kuantum mekaniğinde Schrödinger’in meşhur kedisi örneği vardır: kutunun içindeki kedi gözlem yapılana kadar hem ölü hem diri kabul edilir. Yani sistemin durumu belirsizlik içindedir. Buradaki “süperpozisyon” kavramı bilgi teorisindeki entropiye doğrudan denk olmasa da, ikisi de “bilginin eksikliği → belirsizlik → karmaşa” ortak noktasında buluşur.
Enerji miktarının azalmasıyla entropinin ters orantılı oluşu bizlere “enerjiyi nasıl azaltırız?” gibi zor bir sorudan kurtararak “entropiyi nasıl arttırırız” sorusuna yöneltmiştir. Bu sayede Claude Shannon, bilgi kaybı olmadan bir mesaj göndermek için gereken minimum kodlama boyutunu tanımlamak için entropi terimini icat etmiştir.
Bir olay sık olan bir şeyse → “hiç şaşırtmaz”. Bilgi katkısı küçüktür. Bir olay nadir olan bir şeyse → “sürpriz” → büyük bilgi içerir.
Yani: \(I(A) = -\log p(A)\)Yani: $p(A) = 1$ (kesin olacak şey) → $I(A) = 0$ → bilgi gelmiyor. $p(A)$ çok küçük → $I(A)$ büyük → sürpriz var, bilgi yüksek.
Ancak biz tek olaya değil, tüm sistemin ortalamasına bakıyoruz: \(H(X) = -\sum_{i} p(x_i) \log p(x_i)\) Burası Shannon entropisi.
-
Yani “tüm ihtimallerin toplam belirsizliği”.
-
Olasılıklar eşit dağılmışsa (ör: %50 – %50), entropi maksimum.
-
Tek ihtimale kaymışsa (ör: %100 – %0), entropi minimum.
-
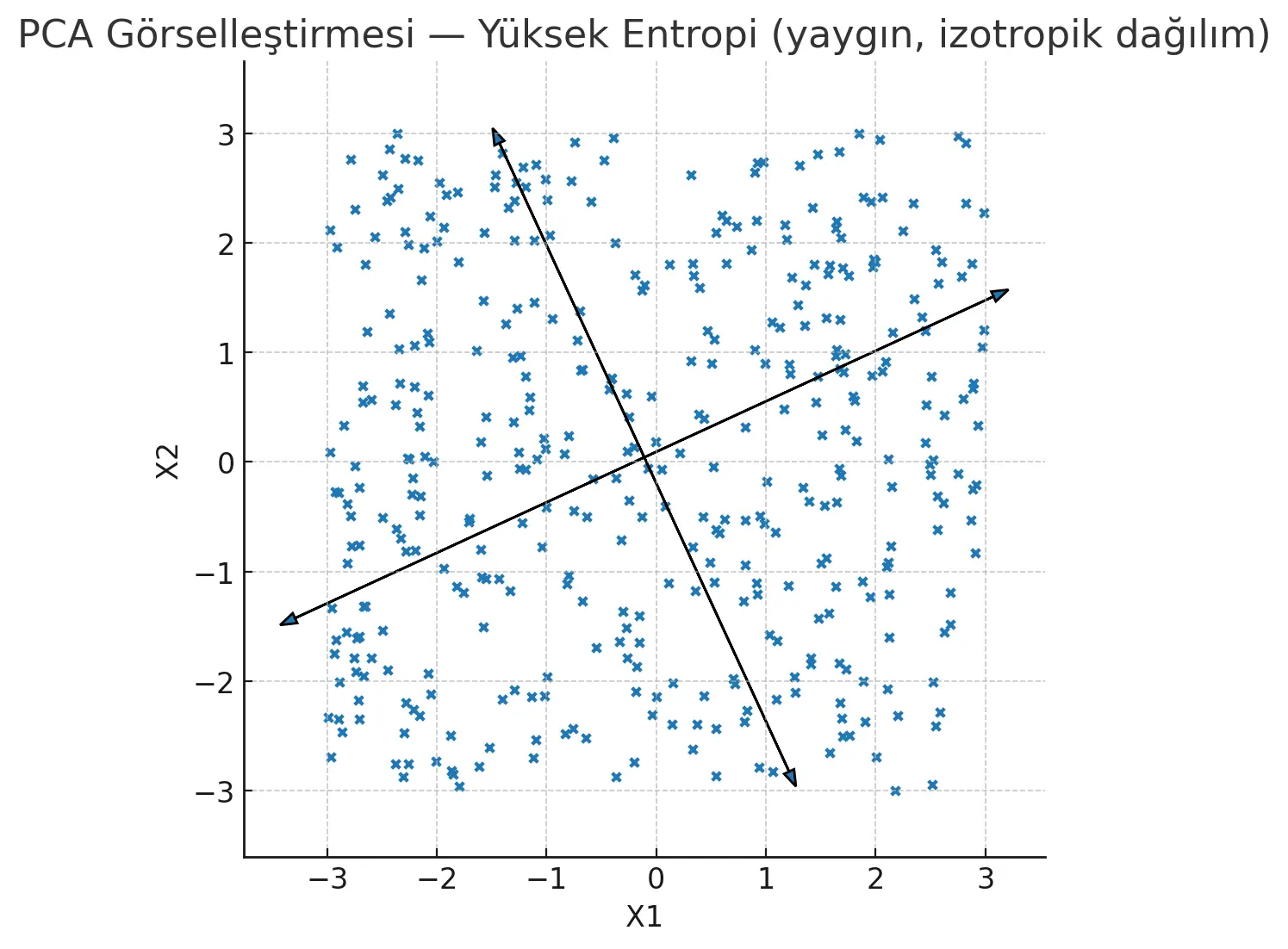
“PCA aslında varyansı maksimize etmeye çalışır. Varyans yüksek → dağılım geniş → entropi de yüksek. Yani bilgi daha çok dağılmış.”
Yukarıda gördüğünüz üzere ilk resimde noktalar her yere dağılmış durumda. Bu bize, sistemin içinde çok fazla farklı ihtimal ve yönelim olduğunu gösteriyor. İkinci resimde ise noktalar tek bir çizgiye dizilmiş gibi; yani herkes aynı şeyi söylüyor. Peki neden ilk resim bize daha çok şey anlatır? Bunu şöyle bir benzetme ile açıklayalım:
Şimdi bunu bir meclis benzetmesiyle düşünelim: Eğ er herkes aynı çizgideyse konuşulacak, tartışılacak bir şey kalmaz. Sistem basit, sıkıcı ve öngörülebilir olur. Ama farklı fikirler, çelişkiler ve çatışmalar varsa meclis kaynar. İşte o kavga, o kaos dediğimiz şey, bizim bilimsel dilde entropi dediğimiz olgudur.
Dolayısıyla yüksek entropi = zenginlik, çeşitlilik, belirsizlik.
Düşük entropi = tekdüzelik, tahmin edilebilirlik.”

Bu çeşitlilik–tekdüzelik meselesi aslında AI modellerinde de birebir karşımıza çıkar. Bir karar ağacının hangi dalı seçeceği ya da bir dil modelinin hangi kelimeyi tahmin edeceği hep bu entropi hesabına bağlıdır
Yapay zekâ ve entropi
Algoritmalar, karar verme süreçlerini optimize etmek, modellerin tahminlerini değerlendirmek ve öğrenme süreçlerini yönlendirmek için entropi temel bir araç olarak kullanır. Bu bağlamda, entropi sadece bir ölçüm aracı olmaktan çıkar, aynı zamanda bir optimizasyon ve güvenilirlik ilkesi olur.
Karar Ağaçları ve Bilgi Kazancı: Veri Belirsizliğini Yönetmek
Karar Ağaçları (Decision Tree), parametrik olmayan ve hem sınıflandırma hem de regresyon problemleri için kullanılan bir gözetimli öğrenme yöntemidir.
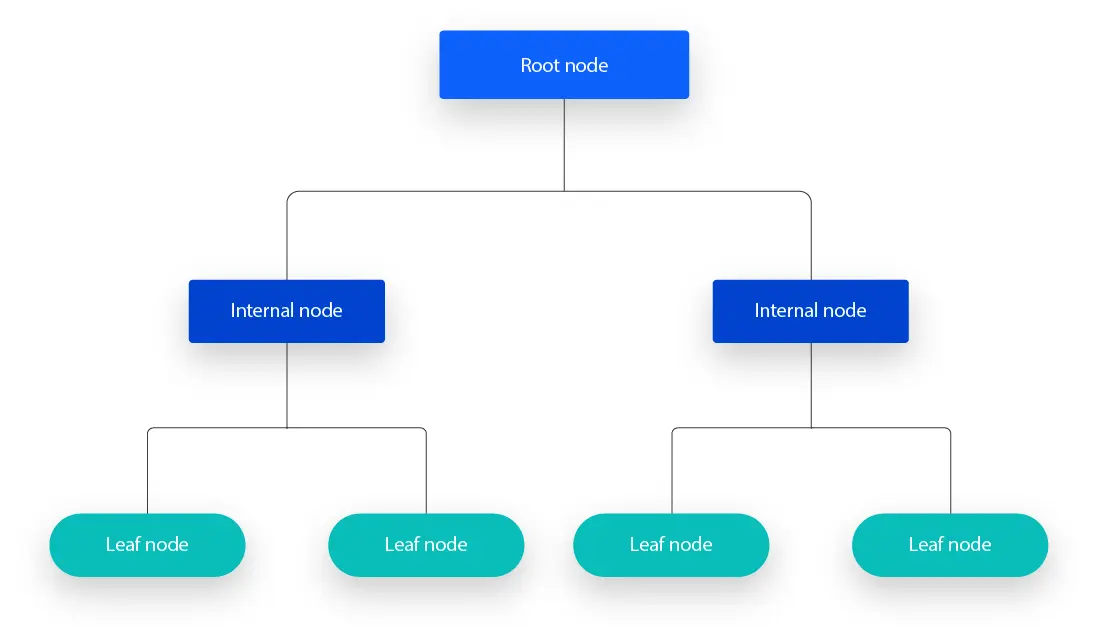
Karar ağaçları bir düğümden (Root Node) başlayarak yeni düğümler ve yapraklar (leaf) oluşturmak üzerine kuruludur. Yeni düğüm ve yaprakların oluşturulması ise entropi ile sağlanır. veri setinde her seferinde basit bir entropi hesabı Bilgi Kazancı (Information Gain) hesaplanır ve bu algoritma bilgi kazancını maksimum, belirsizliği ise minimum düzeyde tutmaya çalışır. Yani bilgi kazancını maksimize edecek özelliği seçer. Karar Ağaçları en açıklanabilir yapay zeka algoritmalarından biridir (XAI, explainable AI).
Çapraz Entropi (Cross-Entropy)
Özellikle sınıflandırma problemlerinde (yani model “hangi sınıf bu?” diye karar verecekse) açık ara en yaygın kullanılan loss çeşididir. Öncelikle kayıp fonksiyonu, yapay zeka modellerinin “ne kadar hatalı” düşündüğünü ölçtüğümüz metriklerdir.
Örneğin, bir modelin kedi, köpek ve kuş sınıflarını içeren bir görseli sınıflandırdığını düşünelim. Eğer görsel bir kedi ise gerçek etiket dağılımı P = [1, 0, 0] olacaktır. Model iyi bir tahmin yapıp Q = [0.8, 0.15, 0.05] olasılıklarını üretirse, çapraz entropi kaybı düşük olacaktır. Ancak, model kötü bir tahmin yaparak Q = [0.25, 0.6, 0.15] (köpeğe yüksek olasılık) gibi bir dağılım üretirse, çapraz entropi kaybı daha yüksek çıkar ve model bu hatayı minimize etmek için ağırlıklarını ayarlar. Bu, modelin sadece doğru cevabı bulmasını değil, aynı zamanda doğru cevaba ne kadar güvenle yaklaştığını da öğrenmesini sağlar.
\[\begin{aligned} H(P,Q) &= -\Big[ 1\cdot\log 0.8 \\ &\quad + 0\cdot\log 0.15 \\ &\quad + 0\cdot\log 0.05 \Big] \\ &= -\log 0.8 \approx 0.22 \end{aligned}\]Cross-entropy, Shannon entropisinin makine öğrenmesindeki uyarlaması gibi çalışıyor. Yani “modelin tahmin dağılımı ile gerçeğin dağılımı arasındaki belirsizlik farkı”nı ölçüyor. Örneğin on sınıflı bir problemde modelin en kötü durumu (yani her sınıfa %10 şans verdiği durumda): $-\log(10) = ~2.3$’tür.
Sonuç
Entropi, bir kavram olarak fizikteki başlangıcından, bilginin soyut dünyasına ve modern yapay zekanın karmaşık algoritmalarına kadar uzanan etkileyici bir yolculuk geçirmiştir. Bu yolculuk boyunca entropi, termodinamiğin evrenin kaderini belirleyen bir yasası olmaktan, enformasyonun kendisini ölçen bir araca ve nihayetinde makine öğrenmesi algoritmalarının temelini oluşturan bir optimizasyon ve güvenilirlik prensibine dönüşmüştür.
| Tanım | Formül | Birim | Kavramsal Anlam | Örnek | Uygulama Alanı |
|---|---|---|---|---|---|
| Termodinamik Entropi | $\Delta S = \dfrac{\delta Q}{T}$ | J/K | Faydasız enerji veya iş potansiyeli kaybı | Sıcak bir nesnenin soğuması | Termodinamik, Kimya Mühendisliği |
| İstatistiksel Mekanik Entropi | $S = k \ln W$ | J/K | Olası mikroskobik durumların sayısı / Düzensizlik | Bir odada yayılan gaz molekülleri | İstatistiksel Fizik |
| Enformasyon Kuramı Entropisi | $H = - \sum p_i \log p_i$ | bit (log₂ tabanı), nat (ln tabanı) | Bir olayın belirsizliği / Bilgi miktarı | Bir yazı tura atışının sonucu | bilgi teorisi, Bilgisayar Bilimi |

.webp)